题目内容
4.已知双曲线中心在原点且一个焦点为F1$(-\sqrt{5}{,^{\;}}0)$,点P位于该双曲线上,线段PF1的中点坐标为(0,2),则双曲线的方程为( )| A. | $\frac{{x}^{2}}{2}$-y2=1 | B. | ${x^2}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ |
分析 设出双曲线的方程,据双曲线的焦点坐标列出三参数满足的一个等式;利用中点坐标公式求出P的坐标,将其坐标代入双曲线的方程,求出三参数的另一个等式,解两个方程得到参数的值.
解答 解:据已知条件中的焦点坐标判断出焦点在x轴上,
∵一个焦点为F1$(-\sqrt{5}{,^{\;}}0)$,
∴a2+b2=5①
∵线段PF1的中点坐标为(0,2),
∴P的坐标为($\sqrt{5}$,4)将其代入双曲线的方程得$\frac{5}{{a}^{2}}-\frac{16}{{b}^{2}}$=1②
解①②得a2=1,b2=4,
所以双曲线的方程为${x}^{2}-\frac{{y}^{2}}{4}$=1.
故选:B.
点评 求圆锥曲线常用的方法:待定系数法、注意双曲线中三参数的关系为:c2=b2+a2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列函数中,与函数y=$\frac{1}{{\sqrt{x}}}$有相同定义域的是( )
| A. | f(x)=lnx | B. | $f(x)=\frac{1}{x}$ | C. | f(x)=|x| | D. | f(x)=ex |
15.已知a、b、c分别为△ABC三个内角A、B、C所对的边长,∠A=60°,且acosB-bcosA=$\frac{3}{5}$c,则$\frac{2absinC}{{a}^{2}+{b}^{2}-{c}^{2}}$=( )
| A. | -5$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
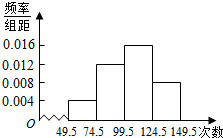 为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.
为了调查学生的课外阅读情况,在某班级对全体学生每天阅读时间(单位:分钟)进行调查,将调查数据整理后,画出频率分布直方图如图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第三组的频数为20.