题目内容
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:依题意,令n=1,2,3,4,得到相应的值,观察,即可猜想出结果,利用裂项相消法求和验证即可.
解答:
解:n=1时,
=
;n=2时,
+
=
+
=
;
n=3时,
+
+
=
+
=
;n=4时,
+
+
+
=
+
=
.
观察所得结果:均为分数,且分子恰好等于和式的项数,分母都比分子大1.
所以猜想
+
+
+…+
=
.
证明如下:
由
=1-
,
=
-
,…,
=
-
,得
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
n=3时,
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 2 |
| 3 |
| 1 |
| 12 |
| 3 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 3 |
| 4 |
| 1 |
| 20 |
| 4 |
| 5 |
观察所得结果:均为分数,且分子恰好等于和式的项数,分母都比分子大1.
所以猜想
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| n |
| n+1 |
证明如下:
由
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查数列的求和,考查推理运算能力,突出列项相消法的考查,属于中档题.

练习册系列答案
相关题目
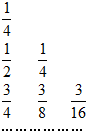 下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).
下表给出一个“三角形数阵”(如图),已知每一列的数成等差数列,从第三行起每一行的公比都相等,记第i行第j列的数为aij(i≥j,i,j∈N*).