题目内容
6．已知cos$\frac{α}{2}$-sin$\frac{α}{2}$=$\frac{1}{5}$，求sinα的值．分析 利用两边平方，通过二倍角的正弦函数求解即可．
解答 解：cos$\frac{α}{2}$-sin$\frac{α}{2}$=$\frac{1}{5}$，
可得1-sinα=$\frac{1}{25}$，
解得sinα=$\frac{24}{25}$．
点评 本题考查三角函数的化简求值，考查计算能力．
练习册系列答案
相关题目
16．函数f（x）是定义在区间（-∞，0）上的可导函数，其导函数为f′（x），且满足xf′（x）＞-2f（x），则不等式$\frac{（x+2015）^{2}f（x+2015）}{16}$＜f（-4）的解集为（ ）
| A． | {x|-2019＜x＜0} | B． | {x|x＜-2019} | C． | {x|-2019＜x＜-2015} | D． | {x|-2011＜x＜0} |
17．寒假里5名同学结伴乘坐成绵乐动车到峨眉山旅游，实名制购票，每人一座，恰在同一排A，B，C，D，E五个座位（一排共五个座位），上车后五人在这五个座位上随意坐，恰有一人人坐对与自己车票相符座位的坐法种数为（ ）
| A． | 15 | B． | 30 | C． | 45 | D． | 90 |
11．
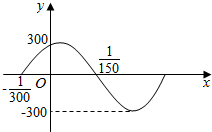如图，表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin（ωt+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象，则该函数解析式是（ ）
如图，表示某简谐运动离开平衡位置的距离y与时间t的关系y=Asin（ωt+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象，则该函数解析式是（ ）| A． | y=300sin（50πt+$\frac{π}{3}$） | B． | y=300sin（50πt-$\frac{π}{3}$） | ||
| C． | y=300sin（100πt+$\frac{π}{3}$） | D． | y=300sin（100πt-$\frac{π}{3}$） |
1．已知函数$f（x）=\frac{sinx}{cosx+1}$，则（ ）
| A． | f（x）的最小正周期是π | B． | f（x）相邻对称中心相距π个单位 | ||
| C． | f（x）相邻渐近线相距π个单位 | D． | f（x）既是奇函数又是增函数 |