题目内容
7.已知函数f(x)=-8sinx+tanx(x∈($-\frac{π}{2}$,$\frac{π}{2}$)),则f(x)为增函数的概率为( )| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 利用函数的导数求得f(x)的单调递增区间,f(x)为增函数的概率即为单调增区间的长度比上总长度.
解答 解:f(x)=-8sinx+tanx,
f′(x)=-8cosx+$\frac{1}{co{s}^{2}x}$=$\frac{1-8co{s}^{3}x}{co{s}^{2}x}$,
f(x)为增函数,f′(x)=$\frac{1-8co{s}^{3}x}{co{s}^{2}x}$>0,
∴cosx<$\frac{1}{2}$,又x∈($-\frac{π}{2}$,$\frac{π}{2}$),
∴x∈(-$\frac{π}{2}$,-$\frac{π}{3}$)∪($\frac{π}{3}$,$\frac{π}{2}$),
f(x)为增函数的概率P=$\frac{\frac{π}{6}×2}{π}$=$\frac{1}{3}$.
故答案选:D.
点评 本题考查古典概型,利用导数求出函数的单调区间,并求出其长度,并求出其与总长度的比值,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
19.已知a=(1-i)(1+bi),其中a,b是实数,i是虚数单位,则$\frac{a+bi}{i}$=( )
| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
16.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-c,0)、F2(c,0),P是椭圆C上一点,且|PF2|=|F1F2|,直线PF1与圆x2+y2=$\frac{{c}^{2}}{4}$相切,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
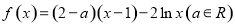 .
. 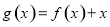 上点
上点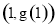 处的切线过点
处的切线过点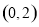 ,求函数
,求函数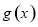 的单调减区间;
的单调减区间; 在
在 上无零点,求
上无零点,求 的最小值.
的最小值.