题目内容
已知函数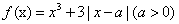 ,
,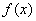 在
在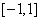 上的最小值记为
上的最小值记为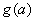 .(1)求
.(1)求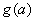 ;(2)证明:当
;(2)证明:当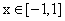 时,恒有
时,恒有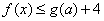 .
.
[解析] (1)因为 ,所以,
,所以,
(i)当 时,若
时,若 ,则
,则 ,
, 故
故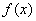 在
在 上是减函数;若
上是减函数;若 ,则
,则 ,
, ,故
,故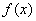 在
在 上是增函数.所以
上是增函数.所以 .
.
(ii)当 时,有
时,有 ,则
,则 ,
, ,故
,故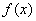 在
在 上是减函数,所以
上是减函数,所以 .综上,
.综上,
(2)证明:令 .(i)当
.(i)当 时,
时,
若 ,则
,则 ,得
,得 ,则
,则 在
在 上是增函数,所以
上是增函数,所以 在
在 上的最大值是
上的最大值是 ,而
,而 ,所以
,所以 ,故
,故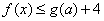 .
.
若 ,则
,则 ,得
,得 ,则
,则 在
在 上是减函数,所以
上是减函数,所以 在
在 上的最大
上的最大 值是
值是 ,令
,令 ,则
,则 ,知
,知 在
在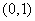 上是增函数,所以
上是增函数,所以 ,即
,即 .故
.故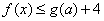 .
.
(ii)当 时,
时, ,故
,故 ,得
,得 ,此时
,此时 在
在 上是减函数,因此
上是减函数,因此 在
在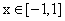 上的最大值是
上的最大值是 .故
.故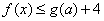 .综上,当
.综上,当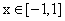 时,恒有
时,恒有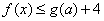 .
.

练习册系列答案
相关题目

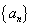 中,若
中,若 ,
, ,则
,则 的值是 .
的值是 . 实数k的取值范围.
实数k的取值范围. 有3个不同的零点,则实数a的取值范围是 .
有3个不同的零点,则实数a的取值范围是 . 有两个极值点,则实数
有两个极值点,则实数 的取值范围是 .
的取值范围是 .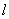 与曲线C满足下列两个条件:
与曲线C满足下列两个条件: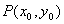 处与曲线C相切;(ii)曲线C在点
处与曲线C相切;(ii)曲线C在点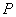 附近位于直线
附近位于直线 :y=x3;
:y=x3;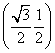 ,当秒针从P0(此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为________.
,当秒针从P0(此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系式为________.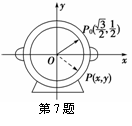
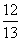 ,cosC=
,cosC=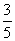 .
.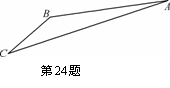
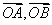 不共线,设
不共线,设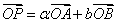 ,
,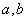 均为实数,且满足
均为实数,且满足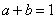 ,求证:
,求证: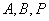 三点共线.
三点共线.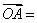 a + 2b,
a + 2b,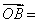 2a + 4b,
2a + 4b,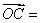 3a + 6b (其中a
3a + 6b (其中a  、b是两个任意非零向量) ,证明:A、B、C三点共线.
、b是两个任意非零向量) ,证明:A、B、C三点共线.