题目内容
18.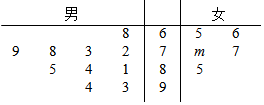 某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.
某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.(I)求男生成绩的中位数及m的值;
(Ⅱ)如果用分层抽样的方法,从一等奖和二等奖学生中共选取5人,再从这5人中选取2人,求至少有1人是一等奖的概率.
分析 (Ⅰ)利用中位数、平均值的意义即可得出;
(Ⅱ)利用分层抽样及列举法、古典概型的计算公式即可得出.
解答 解:(Ⅰ)男生成绩的中位数为$\frac{79+81}{2}$=80,
∵这5名女生的平均成绩为73,
∴$\frac{1}{5}$(65+66+77+(70+m)+85)=73,
解得m=2,
(Ⅱ)由题意知一等奖获得者有6人,二等奖获得者为9人,
则用分层抽样的选取的一等奖人数为$\frac{6}{15}$×5=2人,记为A1,A2,
选取的二等奖的人数为$\frac{9}{15}×5$=3人,记为B1,B2,B3.
从这5人中选2人的所以可能情况为:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(B1,B2),(B1,B3),(B2,B3),共10种,
这10个基本事件是等可能性的,
其中至少有1人是至少有1人是一等奖的结果有7种,
∴至少有1人是一等奖的概率P=$\frac{7}{10}$
点评 本题考查了由茎叶图求数据的平均数及古典概型的概率计算,熟练掌握茎叶图是解答问题的关键.

练习册系列答案
相关题目
7.已知{an}中,${a_n}={n^2}+λn$,且{an}是递增数列,则实数的取值范围是( )
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
3.已知不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≥-1\\ y≥0\end{array}\right.$所表示的平面区域为D,若直线(m+2)x-(m+1)y+2=0与平面区域D有公共点,则实数m的取值范围为( )
| A. | (-4,0) | B. | [-4,0] | C. | (-∞,-4)∪(0,+∞) | D. | (-∞,-4]∪[0,+∞) |
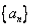 ,满足
,满足 ,则
,则 的最小值为( )
的最小值为( ) 的直线与圆
的直线与圆 相切,则此直线在
相切,则此直线在 轴上的截距是
轴上的截距是  在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.
在如图所示三棱锥D-ABC中,AD⊥DC,AB=4,AD=CD=2,∠BAC=45°,平面ACD⊥平面ABC,E,F分别在BD,BC,且BE=2ED,BC=2BF.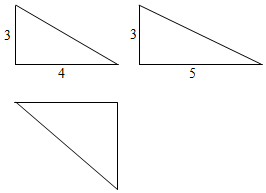 已知一个几何体的三视图图图所示,求该几何体的外接球的表面积50π.
已知一个几何体的三视图图图所示,求该几何体的外接球的表面积50π.