题目内容
5.对于左边2×2列联表,在二维条形图中,两个比例的值$\frac{a}{a+b}$与$\frac{c}{c+d}$相差越大,H:“x 与 Y 有关系”的可能性越大.分析 根据卡方公式,可得数值$\frac{a}{a+b}$与$\frac{c}{c+d}$相差越大,卡方越大,即可得出结论.
解答 解:根据卡方公式,可得数值$\frac{a}{a+b}$与$\frac{c}{c+d}$相差越大,卡方越大,
∴两个变量有关系的可能性就就越大,
故答案为越大.
点评 本题考查独立性检验知识,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
20.一位同学一次投篮的命中率试0.4,我们通过随机模拟的方式来判断这位同学3次投篮的命中情况,用表示命中,用0,1,2,3表示不命中,计算机产生20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这位同学恰有两次命中的概率是( )
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这位同学恰有两次命中的概率是( )
| A. | $\frac{7}{20}$ | B. | $\frac{9}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
5. 如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
 如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )| A. | 8$\sqrt{6}$π | B. | 24π | C. | 32$\sqrt{3}$π | D. | 48π |
9.在正四面体的4个面上分别写着1,2,3,4.将4个这样的均匀正四面体投掷于桌面上,与桌面接触的4个面上的4个数的乘积被4整除的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{9}{64}$ | C. | $\frac{1}{16}$ | D. | $\frac{13}{16}$ |
10.直线y=$\frac{1}{2}$x+b是曲线y=lnx(x>0)的一条切线,则实数b的值为( )
| A. | 2 | B. | ln2+1 | C. | ln2-1 | D. | ln2 |
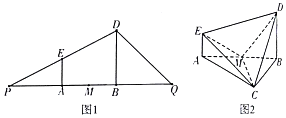 已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.
已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.