题目内容
已知函数f(x)=
(a≠0),当x∈(-∞,1)时,判断函数f(x)单调性,并说明理由.
| a |
| x-1 |
考点:函数单调性的性质
专题:函数的性质及应用
分析:设1>x2>x1,化简 f(x2)-f(x1)为
,再分a>0、a<0两种情况,根据
的符号,可得f(x2)与f(x1) 的大小关系,从而判断函数的单调性
| a(x1-x2) |
| (x2-1)(x1-1) |
| a(x1-x2) |
| (x2-1)(x1-1) |
解答:
解:设1>x2>x1,∵f(x2)-f(x1)=
-
=
,x1-x2<0,x2-1<0,x1-1<0,
∴
<0.
当a>0时,
<0,f(x2)<f(x1),函数f(x)在(-∞,1)上是减函数.
当a<0时,
>0,f(x2)>f(x1),函数f(x)在(-∞,1)上是增函数.
| a |
| x2-1 |
| a |
| x1-1 |
| a(x1-x2) |
| (x2-1)(x1-1) |
∴
| x1-x2 |
| (x2-1)(x1-1) |
当a>0时,
| a(x1-x2) |
| (x2-1)(x1-1) |
当a<0时,
| a(x1-x2) |
| (x2-1)(x1-1) |
点评:本题主要考查函数的单调性的判断和正明,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在下列函数中,最小值是2的是( )
A、y=
| ||||
B、y=
| ||||
C、y=sinx+
| ||||
| D、y=7x+7-x |
设函数f(x)=
的定义域为集合A,集合B={x|x-a+1<0},若A∩B≠∅,则a的取值范围是( )
| x-2 |
| A、a>3 | B、a≥3 |
| C、a<3 | D、a≤3 |
已知函数y=f(x)是定义在(-1,1)上的函数,且对于任意x1,x2∈(-1,1)且x1≠x2,都有
<0,则关于a的不等式f(1-a)<f(a2-1)的取值范围是( )
| f(x1)-f(x2) |
| x 1-x2 |
| A、-2<a<1 | ||
| B、a>1或a<-2 | ||
C、0<a<
| ||
| D、0<a<1 |
由不等式组
所表示的平面区域的面积是( )
|
| A、2 | ||
| B、1 | ||
C、
| ||
| D、4 |
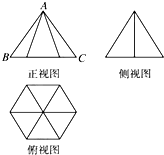 一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的侧视图的面积.
一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的侧视图的面积. 已知程序如图:
已知程序如图: