题目内容
19.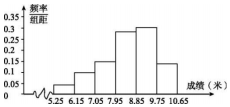 某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记X表示两人中进入决赛的人数,求X的分布列及数学期望;
(Ⅲ)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.
分析 (Ⅰ)由频率分直方图求出第6小组的频率,从而求出总人数,进而得到第4、5、6组成绩均进入决赛,由此能求出进入决赛的人数.
(Ⅱ)由题意知X的可能取值为0,1,2,进入决赛的概率为$\frac{36}{50}=\frac{18}{25}$,从而X~$(2,\frac{18}{25})$,由此能求出X的分布列及数学期望.
(Ⅲ)设甲、乙各跳一次的成绩分别为x、y米,则基本事件满足的区域为:$\left\{\begin{array}{l}{8≤x≤10}\\{9.5≤y≤10.5}\end{array}\right.$,由此利用几何概型能求出甲比乙远的概率.
解答 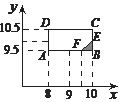 解:(Ⅰ)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,
解:(Ⅰ)第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14,
∴总人数为$\frac{7}{0.14}=50$(人).…(2分)
∴第4、5、6组成绩均进入决赛,人数为(0.28+0.30+0.14)×50=36(人)
即进入决赛的人数为36.…(4分)
(Ⅱ)由题意知X的可能取值为0,1,2,进入决赛的概率为$\frac{36}{50}=\frac{18}{25}$,
∴X~$(2,\frac{18}{25})$,$P({x=0})=C_2^0{(\frac{7}{25})^2}=\frac{49}{625}$,
P(X=1)=${C}_{2}^{1}(\frac{7}{25})(\frac{18}{25})=\frac{252}{625}$,
$P({x=2})=C_2^2{(\frac{18}{25})^2}=\frac{324}{625}$.…(6分)
∴所求分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{49}{625}$ | $\frac{252}{625}$ | $\frac{324}{625}$ |
(Ⅲ)设甲、乙各跳一次的成绩分别为x、y米,
则基本事件满足的区域为:$\left\{\begin{array}{l}{8≤x≤10}\\{9.5≤y≤10.5}\end{array}\right.$,
事件A“甲比乙远的概率”满足的区域为x>y,如图所示.…(10分)
∴由几何概型P(A)=$\frac{\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1×2}$=$\frac{1}{16}$.
即甲比乙远的概率为$\frac{1}{16}$.…(12分)
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列及数学期望的求法,考查概率的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

| A. | {-2,-1,1,2} | B. | {-2,-1,1} | C. | {1} | D. | {1,2} |
| A. | -2 | B. | -i | C. | i | D. | -1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |

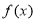 是定义在
是定义在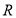 上的偶函数,且在区间
上的偶函数,且在区间 上单调递增,若实数
上单调递增,若实数 满足
满足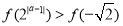 ,则
,则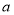 的取值范围是( )
的取值范围是( )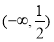 B.
B.
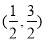 D.
D.
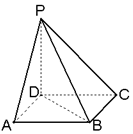 如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.
如图,已知ABCD是正方形,PD⊥平面ABCD,PD=AD.