题目内容
11.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边.若(a+b-c)(a+b+c)=ab,c=$\sqrt{3}$,当ab取得最大值时,S△ABC=$\frac{\sqrt{3}}{4}$.分析 由已知及基本不等式可求ab≤1,当且仅当a=b时取等号,当ab取得最大值时,由余弦定理可求cosC,利用同角三角函数基本关系式可求sinC,进而利用三角形面积公式即可计算得解.
解答 解:∵(a+b-c)(a+b+c)=ab,c=$\sqrt{3}$,
∴(a+b)2-c2=ab,可得:a2+b2=c2-ab=3-ab,
∵a2+b2≥2ab,当且仅当a=b时取等号,
∴3-ab≥2ab,即:ab≤1,当且仅当a=b时取等号,
∴当ab取得最大值时,a=b=1,可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$,sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{\sqrt{3}}{2}$,
可得:S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题主要考查了基本不等式,余弦定理,同角三角函数基本关系式,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
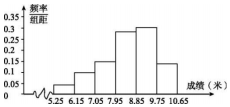 某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7. B.
B.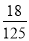
 D.
D.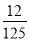
 的增区间为____________.
的增区间为____________.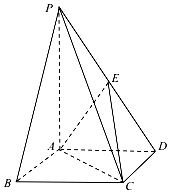 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PA⊥底面ABCD,点E是PD的中点,AB=2,PA=3.