题目内容
4．设i为虚数单位，若复数$\frac{i}{1+i}$的实部为a，复数（1+i）2的虚部为b，则复数z=a-bi在复平面内的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数代数形式的乘除运算化简分别求出a，b的值得答案．
解答 解：∵$\frac{i}{1+i}$=$\frac{i（1-i）}{（1+i）（1-i）}=\frac{1}{2}+\frac{1}{2}i$，∴a=$\frac{1}{2}$，
∵（1+i）2=2i，∴b=2，
则z=a-bi对应点的坐标为（$\frac{1}{2}，-2$），位于第四象限．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
12．从数字1，2，3，4，5中，随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于12的概率为（ ）
| A． | $\frac{2}{25}$ | B． | $\frac{13}{125}$ | C． | $\frac{18}{125}$ | D． | $\frac{9}{125}$ |
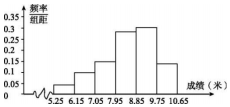某校举行运动会，其中三级跳远的成绩在8.0米（四舍五入，精确到0.1米）以上的进入决赛，把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30，第6小组的频数是7．
9．
某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{π}{3}$ | B． | $\frac{7π}{6}$ | C． | π | D． | $\frac{5π}{6}$ |
对于任意
恒成立； 
，如果命题“
为真，
为假”，求实数
的取值范围．