题目内容
20.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左,右焦点M、N.若以椭圆的焦点为顶点,以椭圆长轴的顶点为焦点作一双曲线恰为等轴双曲线.(1)求椭圆的离心率;
(2)设L为过椭圆右焦点N的直线,交椭圆于P、Q两点,当△MPQ周长为8时;求△MPQ面积的最大值.
分析 (1)由等轴双曲线的性质,即可求得b=c,则a=$\sqrt{2}$c,根据椭圆的离心率公式即可求得椭圆的离心率;
(2)方法一:由4a=8,求得椭圆方程,设直线l的方程,代入椭圆方程,利用韦达定理及弦长公式即可表达出△MPQ面积,换元根据基本不等式的性质,即可求得△MPQ面积的最大值.
方法二:根据对称性,设直线PQ的倾斜角,直线L的方程代入椭圆方程,由椭圆的焦点弦公式,利用韦达定理及基本不等式的性质,即可求得△MPQ面积的最大值;
方法三:根据对称性,设直线PQ的倾斜角,直线L的方程代入椭圆方程,由弦长公式,利用韦达定理及基本不等式的性质,即可求得△MPQ面积的最大值;
解答 解:(1)由题意双曲线为$\frac{x^2}{c^2}-\frac{y^2}{b^2}=1$为等轴双曲线,
则b=c,a2=b2+c2=2c2,即a=$\sqrt{2}$c,
∴椭圆的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
∴椭圆的离心率$\frac{\sqrt{2}}{2}$;(4分)
(2)方法一:△MPQ周长为4a=8,则椭圆为:$\frac{x^2}{4}+\frac{y^2}{2}=1$,(6分)
设PQ为$x=ny+\sqrt{2}$,P(x1,y1),Q(x2,y2),
则$\left\{\begin{array}{l}{x=ny+\sqrt{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,整理得:$({{n^2}+2}){y^2}+2\sqrt{2}ny-2=0$(8分)
由韦达定理$\left\{{\begin{array}{l}{{y_1}+{y_2}=-\frac{{2\sqrt{2}n}}{{{n^2}+2}}}\\{{y_1}•{y_2}=-\frac{2}{{{n^2}+2}}}\end{array}}\right.$,则丨y1-y2丨=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{4\sqrt{2}\sqrt{{n}^{2}+1}}{{n}^{2}+2}$,
$⇒{S_△}=\frac{1}{2}|{MN}||{{y_1}-{y_2}}|=\frac{{4\sqrt{2}\sqrt{{n^2}+1}}}{{{n^2}+2}}$(10分)
令t=$\sqrt{{n}^{2}+1}$≥1;则${S_△}=\frac{{4\sqrt{2}t}}{{{t^2}+2}}=\frac{{4\sqrt{2}}}{{t+\frac{1}{t}}}≤2\sqrt{2}$.(显然当t=1,即n=0时最大),
△MPQ面积的最大值2$\sqrt{2}$.(12分)
法二:由对称性,不妨设PQ的倾斜角为α∈(0,$\frac{π}{2}$].△MPQ面积S,S=$\frac{1}{2}$丨MN丨sinα丨PQ丨,
△MPQ周长为8时可得:椭圆为:$\frac{x^2}{4}+\frac{y^2}{2}=1$,
∴${y_1}+{y_2}=-\frac{{2\sqrt{2}n}}{{{n^2}+2}};{y_1}•{y_2}=-\frac{2}{{{n^2}+2}}$,
设PQ为$x=ny+\sqrt{2}$其中$n=\frac{1}{tanα}$代入椭圆得$({{n^2}+2}){y^2}+2\sqrt{2}ny-2=0$,
又焦点弦$|{PQ}|=a-e{x_1}+a-e{x_2}=2a-e({n{y_1}+\sqrt{2}})-e({n{y_2}+\sqrt{2}})$,
又焦点弦$|{PQ}|=a-e{x_1}+a-e{x_2}=2a-e({n{y_1}+\sqrt{2}})-e({n{y_2}+\sqrt{2}})$,
=2a-2$\sqrt{2}$e-ne(y1+y2),
=2-$\frac{\sqrt{2}}{2}$n(y1+y2),
=2+$\frac{2{n}^{2}}{{n}^{2}+2}$,
=2+$\frac{2}{1+2ta{n}^{2}α}$,
=$\frac{4}{1+si{n}^{2}α}$,
∴${S_△}=\frac{{4\sqrt{2}sinα}}{{1+{{sin}^2}α}}=\frac{{4\sqrt{2}}}{{sinα+\frac{1}{sinα}}}≤2\sqrt{2}$,显然α=90°时取最大.
△MPQ面积的最大值2$\sqrt{2}$.
法三:△MPQ周长为8时即4a=8,a=2可得:椭圆为:$\frac{x^2}{4}+\frac{y^2}{2}=1$,
由对称性,不妨设PQ的倾斜角为α∈(0,$\frac{π}{2}$].△MPQ面积S,S=$\frac{1}{2}$丨MN丨sinα丨PQ丨,
又丨PQ丨=$\frac{eP}{1-ecosα}$+$\frac{eP}{1+ecosα}$(其中$e=\frac{{\sqrt{2}}}{2},P=\frac{b^2}{c}=\sqrt{2}$),
$|{PQ}|=\frac{1}{{1-\frac{{\sqrt{2}}}{2}cosα}}+\frac{1}{{1+\frac{{\sqrt{2}}}{2}cosα}}=\frac{2}{{1-\frac{1}{2}{{cos}^2}α}}=\frac{4}{{1+{{sin}^2}α}}$,
${S_△}=\frac{{4\sqrt{2}sinα}}{{1+{{sin}^2}α}}=\frac{{4\sqrt{2}}}{{sinα+\frac{1}{sinα}}}≤2\sqrt{2}$,显然α=90°时取最大.
△MPQ面积的最大值2$\sqrt{2}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式,基本不等式性质,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | 在x=-1处取得极大值 | B. | 在区间[-1,4]上是增函数 | ||
| C. | 在x=1处取得极大值 | D. | 在区间[1,+∞)上是减函数 |
| A. | 椭圆 | B. | 双曲线 | ||
| C. | 椭圆或双曲线一支 | D. | 抛物线 |
| A. | y=±$\sqrt{3}$x | B. | y=$±\frac{\sqrt{3}}{3}$ | C. | y=±$\frac{1}{3}$x | D. | y=±3x |
| A. | $\frac{\sqrt{2}}{4}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| 收入 x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出 y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.04 万元 | B. | 11.08 万元 | C. | 12.12 万元 | D. | 12.02 万元 |
| A. | $\frac{5}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{11}{13}$ | D. | $\frac{12}{13}$ |
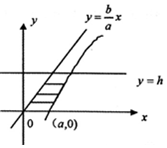 我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.