题目内容
5．双曲线x2-my2=1（m∈R）的右焦点坐标为（2，0），则该双曲线的渐近线方程为（ ）| A． | y=±$\sqrt{3}$x | B． | y=$±\frac{\sqrt{3}}{3}$ | C． | y=±$\frac{1}{3}$x | D． | y=±3x |
分析 根据题意，将双曲线的方程变形可得其标准方程为$\frac{{x}^{2}}{1}-\frac{{y}^{2}}{\frac{1}{m}}$=1，由焦点坐标可得1+$\frac{1}{m}$=4，解可得m的值，即可得双曲线的方程，由渐近线方程可得其渐近线方程．
解答 解：根据题意，双曲线的方程为x2-my2=1，则其标准方程为：$\frac{{x}^{2}}{1}-\frac{{y}^{2}}{\frac{1}{m}}$=1，
其右焦点坐标为（2，0），即c=2，
则有1+$\frac{1}{m}$=4，
解可得m=$\frac{1}{3}$，
故双曲线的方程为x2-$\frac{{y}^{2}}{3}$=1，
其渐近线方程为y=±$\sqrt{3}$x；
故选：A．
点评 本题考查双曲线的几何性质，关键是由焦点坐标求出m的值．
练习册系列答案
相关题目
13．
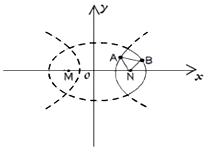有一凸透镜其剖面图（如图）是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1（a＞m＞0）的实线部分组成，已知两曲线有共同焦点M、N；A、B分别在左右两部分实线上运动，则△ANB周长的最小值为（ ）
有一凸透镜其剖面图（如图）是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1（a＞m＞0）的实线部分组成，已知两曲线有共同焦点M、N；A、B分别在左右两部分实线上运动，则△ANB周长的最小值为（ ）| A． | 2（a-m） | B． | （a-m） | C． | 2（b-n） | D． | 2（a+m） |
10．F1，F2分别是双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的左、右焦点，过F2的直线l与双曲线的左右两支分别交于A，B两点，若△ABF1是等边三角形，则该双曲线的虚轴长为（ ）
| A． | 2$\sqrt{6}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{6}$ | D． | 4$\sqrt{2}$ |