题目内容
12.已知抛物线C:y2=4x的焦点是F,过点F的直线与抛物线C相交于P、Q两点,且点Q在第一象限,若2$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则直线PQ的斜率是( )| A. | $\frac{\sqrt{2}}{4}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 过点P,Q分别作抛物线的准线l:x=-1的垂线,垂足分别是P1、Q1,由抛物线的|Q1Q|=|QF|定义可知,|P1P|=|FP|,设|PF|=k(k>0),则|FQ|=2k,在直角△PRQ中求解直线PQ的倾斜角即可求得直线PQ斜率.
解答 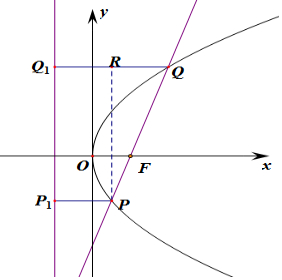 解:过点P,Q分别作抛物线的准线l:x=-1的垂线,垂足分别是P1、Q1,
解:过点P,Q分别作抛物线的准线l:x=-1的垂线,垂足分别是P1、Q1,
由抛物线的定义可知,|Q1Q|=|QF|,|P1P|=|FP|,
设|PF|=k(k>0),2$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则|FQ|=2k,|PQ|=3k,又过点P作PR⊥Q1Q于点R,
则在直角△PRQ中,|RQ|=k,|PQ|=3k,
丨PR丨=$\sqrt{丨PQ{丨}^{2}-丨QR{丨}^{2}}$=2$\sqrt{2}$,
由∠PQR与直线QP的倾斜角相等,
则直线PQ的斜率k=tan∠PQR=$\frac{丨PR丨}{丨QR丨}$=2$\sqrt{2}$,
∴直线PQ的斜率是2$\sqrt{2}$,
故选:D.
点评 本题考查抛物线的简单几何性质及抛物线定义的应用,考查数形结合思想以及计算能力,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
2.在正方体ABCD-A1B1C1D1中,已知$\overrightarrow{{A}_{1}A}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{c}$,O为底面ABCD中心,G为△D1C1O重心,则$\overrightarrow{AG}$=( )(用$\overrightarrow a,\overrightarrow b,\overrightarrow c$表示)
| A. | $\frac{5}{6}\overrightarrow c-\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow a$ | B. | $\frac{5}{6}\overrightarrow c+\frac{1}{2}\overrightarrow b+\frac{2}{3}\overrightarrow a$ | C. | $\frac{5}{6}\overrightarrow c+\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow a$ | D. | $\frac{5}{6}\overrightarrow c-\frac{1}{2}\overrightarrow b+\frac{2}{3}\overrightarrow a$ |
7.下列命题中正确的是( )
| A. | “x<-1”是“x2-x-2>0”的必要不充分条件 | |
| B. | “P且Q”为假,则P假且 Q假 | |
| C. | 命题“ax2-2ax+3>0恒成立”是真命题,则实数a的取值范围是0≤a<3 | |
| D. | 命题“若x2-3x+2=0,则x=2”的否命题为“若x2-3x+2=0,则x≠2” |
4.在锐角三角形△ABC中,a,b,c分别是角A,B,C的对边,${a^2}+{c^2}-{b^2}=\sqrt{3}bc$,则cosA+sinC的取值范围为( )
| A. | $({\frac{3}{2},\sqrt{3}})$ | B. | $({\frac{{\sqrt{3}}}{2},\frac{3}{2}})$ | C. | $({\frac{3}{2},\sqrt{3}}]$ | D. | $({\frac{{\sqrt{3}}}{2},\sqrt{3}})$ |
2.已知α,β,γ为不同的平面,m,n为不同的直线,则m⊥β的一个充分条件是( )
| A. | α∩γ=m,α⊥γ,β⊥γ | B. | α⊥β,β⊥γ,m⊥α | C. | α⊥β,α∩β=n,m⊥n | D. | n⊥α,n⊥β,m⊥α |