题目内容
11.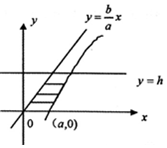 我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
分析 确定AC2-BC2=a2,由祖暅原理知,此旋转体的体积,等价于一个半径为a,高为h的柱体的体积.
解答 解:y=m,是一个圆环其面积
S=π(AC2-BC2)
∵线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1⇒AC2=${a}^{2}+\frac{{a}^{2}}{{b}^{2}}{m}^{2}$,
同理BC2=$\frac{{a}^{2}}{{b}^{2}}{m}^{2}$
∴AC2-BC2=a2,由祖暅原理知,此旋转体的体积,等价于一个半径为a,高为h的柱体的体积为a2hπ.
故答案为:a2hπ.
点评 本题主要考查祖暅原理的应用,求旋转体的体积的方法,体现了等价转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
1.在菱形ABCD中,A=60°,AB=2$\sqrt{3}$,将△ABD沿BD折起到△PBD的位置,若二面角P-BD-C的大小为120°,三棱锥P-BCD的外接球球心为O,BD的中点为E,则OE=( )
| A. | 1 | B. | 2 | C. | $\sqrt{7}$ | D. | 2$\sqrt{7}$ |
2.在正方体ABCD-A1B1C1D1中,已知$\overrightarrow{{A}_{1}A}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{c}$,O为底面ABCD中心,G为△D1C1O重心,则$\overrightarrow{AG}$=( )(用$\overrightarrow a,\overrightarrow b,\overrightarrow c$表示)
| A. | $\frac{5}{6}\overrightarrow c-\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow a$ | B. | $\frac{5}{6}\overrightarrow c+\frac{1}{2}\overrightarrow b+\frac{2}{3}\overrightarrow a$ | C. | $\frac{5}{6}\overrightarrow c+\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow a$ | D. | $\frac{5}{6}\overrightarrow c-\frac{1}{2}\overrightarrow b+\frac{2}{3}\overrightarrow a$ |
19.若(1+2x)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,则a0+a1+a3+a5=( )
| A. | 364 | B. | 365 | C. | 728 | D. | 730 |