题目内容
19.已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1,圆C2:x2+y2=t经过椭圆C1的焦点.(1)设P为椭圆上任意一点,过点P作圆C2的切线,切点为Q,求△POQ面积的取值范围,其中O为坐标原点;
(2)过点M(-1,0)的直线l与曲线C1,C2自上而下依次交于点A,B,C,D,若|AB|=|CD|,求直线l的方程.
分析 (1)由题意的焦点坐标,求得t的值,则丨PO丨∈[2,$\sqrt{6}$],利用三角形的面积公式,即可求得△POQ面积的取值范围;
(2)将直线l的方程,代入椭圆方程及圆的方程,利用韦达定理及向量数量积的坐标运算,即可求得m的值,求得直线直线l的方程.
解答 解:(1)椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1的焦点坐标为(±$\sqrt{2}$,0),则t=2,…(1分)
设P(x,y),则丨PO丨=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{x}^{2}+4-\frac{2}{3}{x}^{2}}$=$\sqrt{4+\frac{{x}^{2}}{3}}$,
由x2∈[0,6],则丨PO丨∈[2,$\sqrt{6}$],…(3分)
则△POQ面积S,S=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{丨PO{丨}^{2}-2}$∈[1,$\sqrt{2}$],
△POQ面积的取值范围[1,$\sqrt{2}$];…(5分)
(2)设直线l的方程为:x=my-1;
联立$\left\{\begin{array}{l}{x=my-1}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,消去x,整理得(2m2+3)y2-4my-10=0,
设A(x1,y1),D(x2,y2),则y1+y2=$\frac{4m}{2{m}^{2}+3}$…(7分)
联立$\left\{\begin{array}{l}{x=my-1}\\{{x}^{2}+{y}^{2}=2}\end{array}\right.$,消去x,得(m2+1)y2-2my-1=0,
设B(x3,y3),D(x3,y4),则y3+y4=$\frac{2m}{{m}^{2}+1}$,…(9分)
又丨AB丨=丨CD丨,则$\overrightarrow{AB}$=$\overrightarrow{CD}$,即y3-y1=y2-y4,…(10分)
从而y1+y2=y3+y4,即$\frac{4m}{2{m}^{2}+3}$=$\frac{2m}{{m}^{2}+1}$,解得m=0,
∴直线l的方程为x=-1.…(12分)
点评 本题考查椭圆的简单几何性质,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
| A. | 60 | B. | 90 | C. | 120 | D. | 180 |
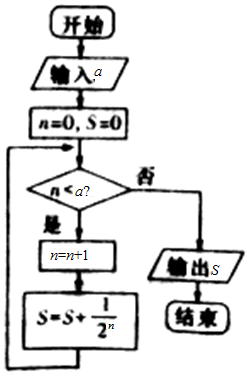
| A. | $\frac{15}{16}$ | B. | $\frac{31}{16}$ | C. | $\frac{31}{32}$ | D. | $\frac{63}{32}$ |
| A. | {0,1,2} | B. | {-1,1,2} | C. | {-1,0,2} | D. | {-1,0,1} |

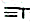 ”表示36,“
”表示36,“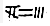 ”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )
”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )


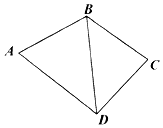 四边形ABCD如图所示,已知AB=BC=CD=2,AD=2$\sqrt{3}$.
四边形ABCD如图所示,已知AB=BC=CD=2,AD=2$\sqrt{3}$.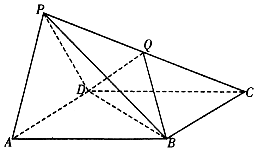 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{7}$,PB=3.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{7}$,PB=3.