题目内容
函数y=f（x）是定义在（-∞，+∞）上的奇函数．若x＞0时、f（x）=log
x，则f（-2）+f（0）= ．
| 1 |
| 2 |
考点：函数奇偶性的性质,对数的运算性质
专题：函数的性质及应用
分析：由题意可得f（0）=0，f（-2）=-f（2）=1，相加可得答案．
解答：
解：∵函数y=f（x）是定义在（-∞，+∞）上的奇函数，∴f（0）=0，
又∵x＞0时、f（x）=log
x，∴f（-2）=-f（2）=1，
∴f（-2）+f（0）=1，
故答案为：1．
又∵x＞0时、f（x）=log
| 1 |
| 2 |
∴f（-2）+f（0）=1，
故答案为：1．
点评：本题考查函数的奇偶性，属基础题．
练习册系列答案
53随堂测系列答案
相关题目
已知数列{an}的前n项和为Sn，且Sn=2an-2，则a2等于（ ）
| A、4 | B、2 | C、1 | D、-2 |
过双曲线
-
=1，（a＞0，b＞0）的右焦点F作垂直于x轴的直线，交双曲线的渐近线于A、B两点，若△OAB（O为坐标原点）是等边三角形，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
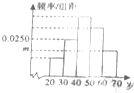为了“城市品位、方便出行、促进发展”，近年合肥市正在修建地铁1号线，市某部门问卷调查了n个市民，其中赞城修建地铁的市民占80%，在赞城修建地铁的市民中又按年龄分组，得样本频率分布直方图如图，其中年龄在[30，40]岁的有2500人，年龄在[60，70）岁的有2000人，则m，n的值分别为（ ）| A、0.2，12500 |
| B、0.2，10000 |
| C、0.02，12500 |
| D、0.02，10000 |
下列说法错误的是（ ）
| A、两两相交且不过同一点的三条直线必在同一平面内 |
| B、过直线外一点有且只有一个平面与已知直线垂直 |
| C、如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直 |
| D、如果两条直线和一个平面所成的角相等，则这两条直线一定平行 |
下列命题中是假命题的是（ ）
| A、?a，b∈R*，lg（a+b）≠lga+lgb |
| B、?φ∈R，使得函数f（x）=sin（2x+φ）是偶函数 |
| C、?α，β∈R，使得cos（α+β）=cosα+cosβ |
| D、?m∈R，使f（x）=（m-1）•x m2-2m+3是幂函数，且在（0，+∞）上递减 |