题目内容
(本题满分18分)本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列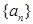 满足
满足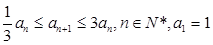 .
.
(1)若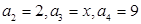 ,求
,求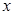 的取值范围;
的取值范围;
(2)若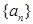 是等比数列,且
是等比数列,且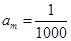 ,正整数
,正整数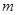 的最小值,以及
的最小值,以及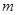 取最小值时相应
取最小值时相应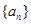 的仅比;
的仅比;
(3)若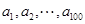 成等差数列,求数列
成等差数列,求数列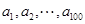 的公差的取值范围.
的公差的取值范围.
(1) ;(2)
;(2) ;(3)
;(3) 的最大值为1999,此时公差为
的最大值为1999,此时公差为 .
.
解析试题分析:(1)比较容易,只要根据已知列出不等式组 ,即可解得;(2)首先由已知得不等式
,即可解得;(2)首先由已知得不等式 ,即
,即 ,可解得
,可解得 。又由条件
。又由条件 ,
, ,于是
,于是 ,取常用对数得
,取常用对数得 ,
, ,所以
,所以 ,即
,即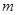 最小值为8;(3)由已知可得∴
最小值为8;(3)由已知可得∴ ,∴
,∴ ,
, ,这样我们可以计算出
,这样我们可以计算出 的取值范围是
的取值范围是 .
.
试题解析:(1)由题得,
(2)由题得,∵ ,且数列
,且数列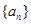 是等比数列,
是等比数列, ,
,
∴ ,∴
,∴ ,∴
,∴ .
.
又由已知 ,∴
,∴ ,又∵
,又∵ ,∴
,∴
∴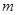 的最小值为8,此时
的最小值为8,此时 ,即
,即 。
。
(3)由题得,∵ ,且数列数列
,且数列数列 成等差数列,
成等差数列, ,
,
∴ ,∴
,∴ ,∴
,∴
【考点】解不等式(组),数列的单调性,分类讨论,等差(比)数列的前 项和.
项和.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 的通项
的通项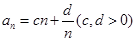 ,第2项是最小项,则
,第2项是最小项,则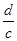 的取值范围是 .
的取值范围是 .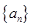 满足:
满足: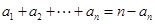 ,其中
,其中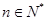 .
.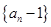 是等比数列;
是等比数列;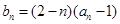 ,求数列
,求数列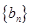 的最大项.
的最大项. 中,
中,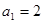 ,对
,对 总有
总有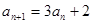 成立,
成立,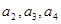 的值;
的值;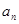 ,并用数学归纳法证明
,并用数学归纳法证明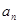 }满足
}满足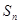 +
+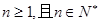 )
)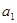 ,
,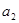 ,
,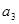 的值;
的值;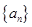 满足:
满足: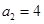 ,公比
,公比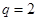 ,数列
,数列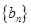 的前
的前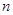 项和为
项和为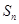 ,且
,且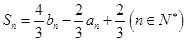 .
.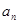 和
和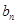 ;
;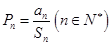 ,证明:
,证明: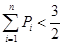 .
.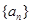 和
和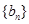 的通项公式分别为
的通项公式分别为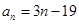 ,
,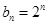 .将
.将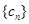 .
.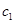 ,
,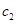 ,
,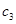 ,
,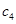 的值,并由此归纳数列
的值,并由此归纳数列 an.
an.