题目内容
已知数列{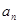 }满足
}满足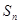 +
+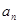 =2n+1 (
=2n+1 (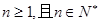 )
)
(1)求出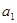 ,
,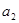 ,
,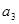 的值;
的值;
(2)由(1)猜想出数列{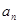 }的通项公式
}的通项公式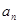 ,并用数学归纳法证明.
,并用数学归纳法证明.
(1)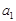 =
=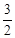 ,
,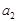 =
=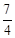 ,
,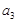 =
=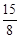 ;(2)
;(2)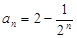
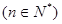 .
.
解析试题分析:解“归纳-猜想-证明”题的关键环节一般有三步,首先准确计算出前若干项,这是归纳,猜想的基础.而后通过观察,分析,比较,联想,猜想出一般结论.最后用数学归纳法证明.(1)由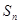 +
+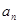 =2n+1,逐一求出各项;(2)由前三项猜想出通项公式
=2n+1,逐一求出各项;(2)由前三项猜想出通项公式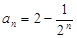 ,用数学归纳法证明过程中,当
,用数学归纳法证明过程中,当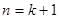 时,所得式子为
时,所得式子为 ,将
,将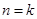 时代入可证.
时代入可证.
解:(1)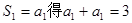 所以
所以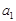 =
=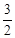 , 又
, 又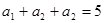 得
得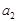 =
=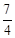 ,同理
,同理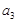 =
=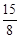 .
.
(2) 猜测
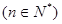 ,
,
(数学归纳法)①由(1)当n=1时,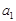 =
=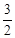 命题成立;
命题成立;
②假设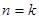 时,
时, 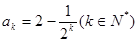 成立,
成立,
则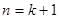 时, 由已知
时, 由已知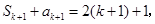
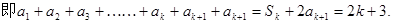
把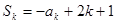 及
及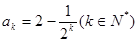 代入化简,
代入化简,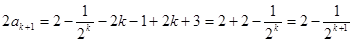 ,
,
即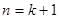 时,命题成立,
时,命题成立,
由①-②得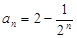
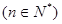 .
.
考点:数列的通项公式,数学归纳法.

练习册系列答案
相关题目
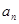 }的通项公式为
}的通项公式为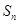 达到最小时,n等于_________________.
达到最小时,n等于_________________. (
(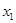 ,
,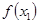 ),
), (
( ,
,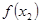 )是函数
)是函数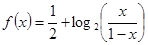 的图象上的任意两点.
的图象上的任意两点.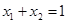 时,求
时,求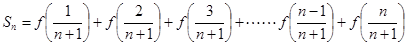 ,其中
,其中 ,求
,求
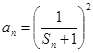 ,其中
,其中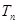 为数列
为数列 的前
的前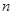 项和,求证
项和,求证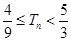 .
.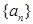 满足
满足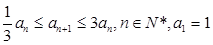 .
.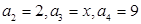 ,求
,求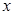 的取值范围;
的取值范围;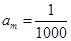 ,正整数
,正整数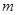 的最小值,以及
的最小值,以及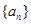 的仅比;
的仅比;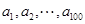 成等差数列,求数列
成等差数列,求数列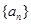 的前
的前 项和
项和 。
。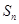 的最大或最小值.
的最大或最小值.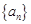 满足:
满足: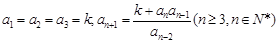 其中
其中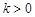 ,数列
,数列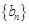 满足:
满足: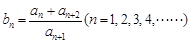
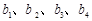 ;
; ,
,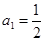 ,且满足
,且满足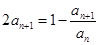 .
. 是等差数列;
是等差数列;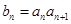 ,求数列
,求数列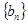 的前n项和
的前n项和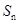 .
.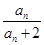 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(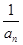 +1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )