题目内容
已知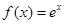 ,
,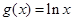 .
.
(Ⅰ)求证: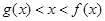 ;
;
(Ⅱ)设直线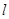 与
与 、
、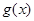 均相切,切点分别为(
均相切,切点分别为(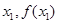 )、(
)、(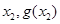 ),且
),且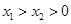 ,求证:
,求证: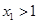 .
.
(Ⅰ) 见解析;(Ⅱ)见解析.
解析试题分析:(Ⅰ)先构造函数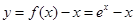 ,利用函数的单调性与导数的关系,求得函数的最小值是
,利用函数的单调性与导数的关系,求得函数的最小值是 ,找到关系
,找到关系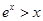 ;再构造函数
;再构造函数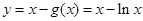 ,利用函数的单调性与导数的关系,求得函数的最小值是
,利用函数的单调性与导数的关系,求得函数的最小值是 ,找到关系
,找到关系 .从而证得“
.从而证得“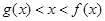 ”;(Ⅲ)先求出
”;(Ⅲ)先求出 以及
以及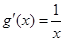 ,根据导数与切线方程的关系,由斜率不变得到
,根据导数与切线方程的关系,由斜率不变得到 ,再根据两点间的斜率公式得到
,再根据两点间的斜率公式得到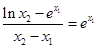 .首先由指数函数的性质可得
.首先由指数函数的性质可得 ,那么
,那么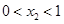 ,然后由
,然后由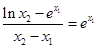 得到
得到 ,解得
,解得 .
.
试题解析:(Ⅰ)令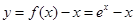 ,
, . 1分
. 1分
令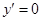 ,解得
,解得 .
.
当 时,
时,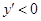 ;当
;当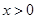 ,时
,时 .
.
∴当 时,
时, ,
,
∴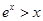 . 3分
. 3分
令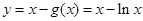 ,
,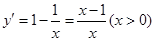 . 4分
. 4分
令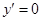 ,解得
,解得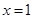 .
.
当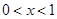 时,
时,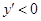 ;当
;当 时,
时, .
.
∴当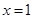 时,
时, ,
,
∴ , 6分
, 6分
∴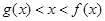 . 7分
. 7分
(Ⅲ) ,
,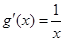 ,切点的坐标分别为
,切点的坐标分别为 ,可得方程组:
,可得方程组: 11分
11分
∵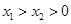 ,
,
∴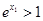 ,∴
,∴ ,
,
∴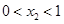 . 12分
. 12分
由②得,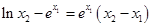 ,∴
,∴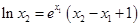 , 13分
, 13分
∵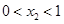 ,∴
,∴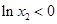 ,∴
,∴ ,即
,即 ,
,
∴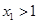 . 14分
. 14分
考点:1.分类讨论思想;2.函数的单调性与导数的关系;3.对数函数的性质;4.指数函数的性质;5.利用导数研究曲线的切线方程

练习册系列答案
相关题目
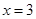 是函数
是函数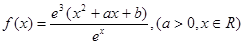 的一个极值点.
的一个极值点. 与
与 的关系式(用
的关系式(用 的单调递增区间;
的单调递增区间;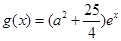 ,若存在
,若存在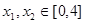 使得
使得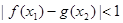 成立,求实数
成立,求实数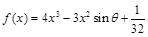 ,其中
,其中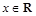 ,
,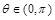 .
.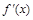 的最小值为
的最小值为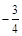 ,试判断函数
,试判断函数 的零点个数,并说明理由;
的零点个数,并说明理由;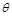 的取值范围.
的取值范围.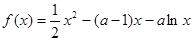 ,
,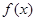 的单调区间;
的单调区间;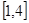 内的最小值为
内的最小值为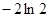 ,求
,求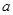 的值.(参考数据
的值.(参考数据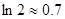 )
)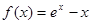 (
(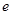 为自然对数的底)
为自然对数的底) 的最小值;
的最小值;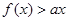 的解集为
的解集为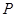 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
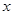 元/本(9≤
元/本(9≤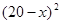 万本.
万本.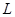 (万元)与每本书的定价
(万元)与每本书的定价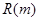 .
.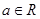 ,函数
,函数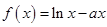 .
.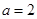 ,求曲线
,求曲线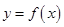 在点
在点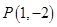 处的切线方程;
处的切线方程; 无零点,求实数
无零点,求实数 的取值范围;
的取值范围; 、
、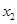 ,求证:
,求证: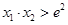 .
.