题目内容
设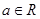 ,函数
,函数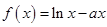 .
.
(1)若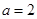 ,求曲线
,求曲线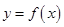 在点
在点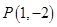 处的切线方程;
处的切线方程;
(2)若 无零点,求实数
无零点,求实数 的取值范围;
的取值范围;
(3)若 有两个相异零点
有两个相异零点 、
、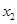 ,求证:
,求证: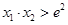 .
.
(1)切线方程为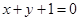 ;(2)实数
;(2)实数 的取值范围是
的取值范围是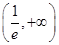 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)将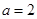 代入函数
代入函数 的解析式,利用导函数的几何意义,结合直线的点斜式求出切线的方程;(2)先求出函数
的解析式,利用导函数的几何意义,结合直线的点斜式求出切线的方程;(2)先求出函数 的导数,对
的导数,对 的符号进行分类讨论,结合零点存在定理判断函数
的符号进行分类讨论,结合零点存在定理判断函数 在定义域上是否有零点,从而求出参数
在定义域上是否有零点,从而求出参数 的取值范围;另外一中方法是将问题等价转化为“直线
的取值范围;另外一中方法是将问题等价转化为“直线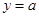 与曲线
与曲线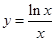 无公共点”,结合导数研究函数
无公共点”,结合导数研究函数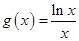 的基本性质,然后利用图象即可确定实数
的基本性质,然后利用图象即可确定实数 的取值范围;(3)从所证的不等式出发,利用分析法最终将问题等价转换为证明不等式
的取值范围;(3)从所证的不等式出发,利用分析法最终将问题等价转换为证明不等式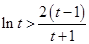 在区间
在区间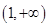 上恒成立,并构造新函数
上恒成立,并构造新函数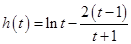 ,利用导数结合函数的单调性与最值来进行证明.
,利用导数结合函数的单调性与最值来进行证明.
试题解析:在区间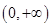 上,
上,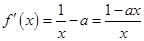 ,
,
(1)当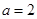 时,
时,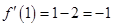 ,则切线方程为
,则切线方程为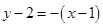 ,即
,即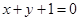 ;
;
(2)①当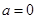 时,
时,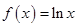 有唯一零点
有唯一零点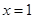 ;
;
②当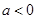 时,则
时,则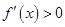 ,
, 是区间
是区间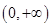 上的增函数,
上的增函数,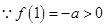 ,
, ,
,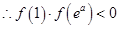 ,即函数
,即函数 在区间
在区间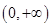 有唯一零点;
有唯一零点;
③当 时,令
时,令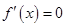 得
得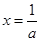 ,
,
在区间 上,
上,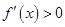 ,函数
,函数 是增函数,
是增函数,
在区间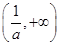 上,
上,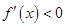 ,函数
,函数 是减函数,
是减函数,
故在区间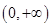 上,
上, 的极大值为
的极大值为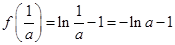 ,
,
由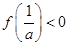 ,即
,即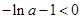 ,解得
,解得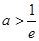 ,故所求实数
,故所求实数 的取值范围是
的取值范围是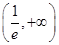 ;
;
另解: 无零点
无零点 方程
方程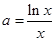 在
在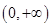 上无实根
上无实根 直线
直线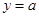 与曲线
与曲线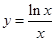 无公共点,
无公共点,
令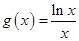 ,则
,则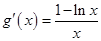 ,令
,令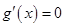 ,解得
,解得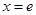 ,列表如下:
,列表如下: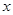



金牌1号名优测试卷系列答案
培生新课堂同步训练与单元测评系列答案
中考系列红十套系列答案
中考新方向系列答案
中考新航线系列答案
专项新评价中考二轮系列答案
中考研究全国各省市中考真题常考基础题系列答案
中考通系列答案
中考添翼中考总复习系列答案
中考题库系列答案
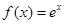 ,
,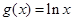 .
.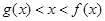 ;
;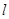 与
与 、
、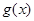 均相切,切点分别为(
均相切,切点分别为(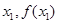 )、(
)、(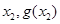 ),且
),且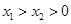 ,求证:
,求证: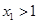 .
.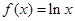 ,
,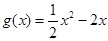 .
.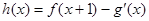 (其中
(其中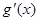 是
是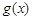 的导函数),求
的导函数),求 的最大值;
的最大值;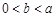 时,有
时,有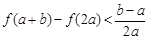 ;
;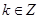 ,当
,当 时,不等式
时,不等式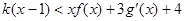 恒成立,求
恒成立,求 的最大值.
的最大值.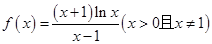 ,
, 的单调性;
的单调性;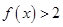 .
.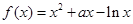 ,
, ;
; 时,求函数
时,求函数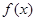 的单调区间;
的单调区间;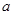 的取值范围;
的取值范围;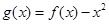 ,是否存在实数
,是否存在实数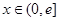 (
(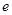 是自然对数的底数)时,函数
是自然对数的底数)时,函数 的最小值是
的最小值是 .若存在,求出
.若存在,求出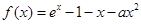 .
.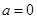 ,求
,求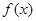 的单调区间;
的单调区间;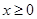 时
时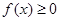 ,求
,求 的取值范围
的取值范围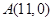 ,函数
,函数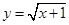 的图象上的动点
的图象上的动点 在
在 轴上的射影为
轴上的射影为 ,且点
,且点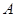 的左侧.设
的左侧.设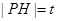 ,
,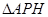 的面积为
的面积为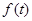 .
.
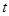 的取值范围;
的取值范围;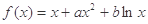 ,曲线
,曲线 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.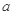 ,
,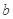 的值;
的值;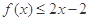 .
.
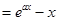 ,其中
,其中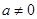 .
.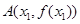 ,
,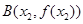
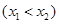 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使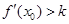 成立?若存在,求
成立?若存在,求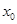 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.