题目内容
已知函数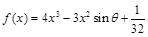 ,其中
,其中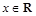 ,
,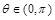 .
.
(Ⅰ)若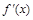 的最小值为
的最小值为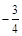 ,试判断函数
,试判断函数 的零点个数,并说明理由;
的零点个数,并说明理由;
(Ⅱ)若函数 的极小值大于零,求
的极小值大于零,求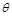 的取值范围.
的取值范围.
(I)函数 的零点个数有3个;(Ⅱ)
的零点个数有3个;(Ⅱ)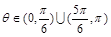
解析试题分析:(I)为确定函数零点的个数,可通过研究函数图象的形态、函数的单调性完成,具体遵循“求导数、求驻点、分区间讨论导数的正负、确定函数的单调性”等步骤.
(Ⅱ)为确定函数的极值,往往遵循“求导数、求驻点、分区间讨论导数的正负、确定函数的极值”等步骤.
本小题利用“表解法”,形象直观,易于理解.为使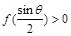 ,
,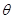 满足
满足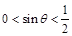 ,从而得到
,从而得到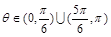 .
.
试题解析:
(I)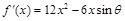 , 1分
, 1分
当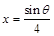 时,
时,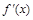 有最小值为
有最小值为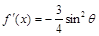 ,
,
所以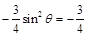 ,即
,即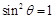 , 2分
, 2分
因为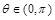 ,所以
,所以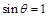 , 3分
, 3分
所以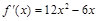 ,
,
所以 在
在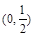 上是减函数,在
上是减函数,在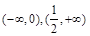 上是增函数, 4分
上是增函数, 4分
而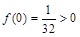 ,
,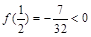 , 5分
, 5分
故函数 的零点个数有3个; 6分
的零点个数有3个; 6分
(Ⅱ)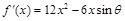 令
令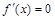 ,得
,得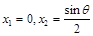 , 7分
, 7分
由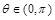 知
知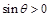 ,根据(I),当
,根据(I),当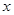 变化时,
变化时,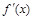 的符号及
的符号及 的变化情况如下表:
的变化情况如下表: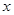
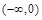
0 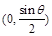
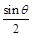
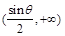
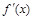
+ 0 - 0 + 
↗ 极大值 ↘  练习册系列答案
练习册系列答案
培优新题库系列答案
教材备考笔记系列答案
竖式计算卡系列答案

名校直通车系列答案
初中学业水平考查系列答案
实验活动练习册系列答案
题优讲练测系列答案
中考快递3年真题荟萃系列答案
中考快递真题28套系列答案
相关题目
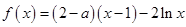 ,
,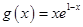 (
( ,
,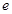 为自然对数的底数).
为自然对数的底数).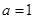 时,求
时,求 的单调区间;
的单调区间;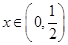 ,
,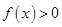 恒成立,求
恒成立,求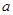 的最小值;
的最小值;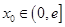 ,在
,在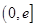 上总存在两个不同的
上总存在两个不同的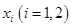 ,使得
,使得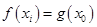 成立,求
成立,求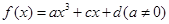 是R上的奇函数,当
是R上的奇函数,当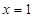 时
时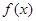 取得极值
取得极值 .
.
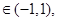 不等式
不等式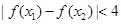 恒成立.
恒成立.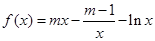 ,
, 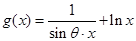 在
在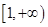 上为增函数,且
上为增函数,且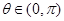 ,求解下列各题:
,求解下列各题: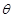 的取值范围;
的取值范围;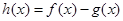 在
在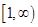 上为单调增函数,求
上为单调增函数,求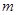 的取值范围;
的取值范围;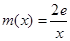 ,若在
,若在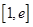 上至少存在一个
上至少存在一个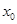 ,使得
,使得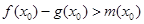 成立,求
成立,求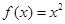 ,
,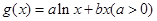 .
.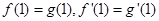 ,求
,求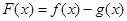 的极小值;
的极小值;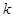 和
和 ,使得
,使得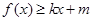 和
和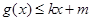 ?若存在,求出
?若存在,求出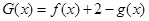 有两个零点
有两个零点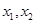 ,且
,且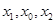 成等差数列,试探究
成等差数列,试探究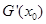 值的符号.
值的符号.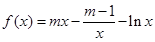 ,
, 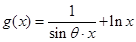 在
在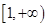 上为增函数,且
上为增函数,且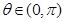 ,求解下列各题:
,求解下列各题: 的取值范围;
的取值范围; 在
在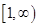 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;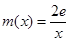 ,若在
,若在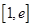 上至少存在一个
上至少存在一个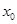 ,使得
,使得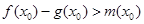 成立,求
成立,求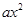 -(a+2)x+lnx.
-(a+2)x+lnx.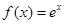 ,
,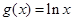 .
.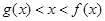 ;
;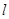 与
与 、
、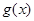 均相切,切点分别为(
均相切,切点分别为(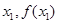 )、(
)、(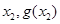 ),且
),且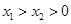 ,求证:
,求证: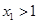 .
.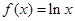 ,
,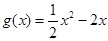 .
.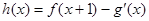 (其中
(其中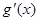 是
是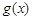 的导函数),求
的导函数),求 的最大值;
的最大值;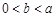 时,有
时,有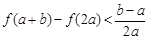 ;
;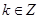 ,当
,当 时,不等式
时,不等式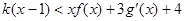 恒成立,求
恒成立,求 的最大值.
的最大值.