题目内容
已知定义在R上的函数y=f(x)满足f(x+2)=f(x),当x∈(-1,1]时,f(x)=x,则函数y=f(x)的图象与函数y=log3|x|的图象的交点的个数是 .
考点:函数的周期性
专题:数形结合,三角函数的图像与性质
分析:根据函数周期性的概念,奇偶性,作出图象,再利用两个图象求出交点个数.
解答:
解:∵在R上的函数y=f(x)满足f(x+2)=f(x),f(x)周期T=2,函数y=log3|x|是偶函数.作图可得在y轴右侧1个交点,y轴左侧2个交点
故答案为:3
故答案为:3
点评:本题考查了函数的奇偶性,周期性,在图象中的应用,运用数形结合思想解决.

练习册系列答案
相关题目
设
,
是两个非零向量,下列能推出
=
的是( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、|
|
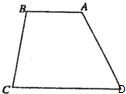 如图所示,有一块四边形的空、地,现欲把它绿化,需知道其面积,以便估算费用.现测得AB=5m,AD=CD=19m,BC=16m,∠ADC=60°.则这块四边形空地的面积是
如图所示,有一块四边形的空、地,现欲把它绿化,需知道其面积,以便估算费用.现测得AB=5m,AD=CD=19m,BC=16m,∠ADC=60°.则这块四边形空地的面积是 如图是函数y=f(x)的导函数f′(x)的图象,对下列四个命题:其中正确的命题是
如图是函数y=f(x)的导函数f′(x)的图象,对下列四个命题:其中正确的命题是