题目内容
以3、4、5为边长的直角三角形，各边分别增加x（x＞0）个单位，得到的三角形一定是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角或钝角三角形 |
考点：三角形的形状判断
专题：计算题,解三角形
分析：求得增加x个单位后的三边，运用余弦定理，求出最大边所对的角的余弦值，计算即可判断三角形的形状．
解答：
解：各边分别增加x个单位后的三边分别为x+3，x+4，x+5，
其最长边所对角的余弦值为
=
＞0，
即有得到的三角形的最大内角为锐角，
所以得到的三角形为锐角三角形．
故选：A．
其最长边所对角的余弦值为
| (x+3)2+(x+4)2-(x+5)2 |
| 2(x+3)(x+4) |
| x2+4x |
| 2(x+3)(x+4) |
即有得到的三角形的最大内角为锐角，
所以得到的三角形为锐角三角形．
故选：A．
点评：本题考查三角形形状的判断，考查余弦定理的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知点P（2，-1）在直线l：ax+y-b=0上的射影是点Q（-2，3），则实数a、b的值依次是（ ）
| A、-1，5 | B、-1，-5 |
| C、1，5 | D、1，-5 |
古代“五行”学认为：“物质分金、木、土、水、火五种属性，金克木，木克土，土克水，水克火，火克金．”将五种不同属性的物质任意排成一列，但排列中属性相克的两种物质不相邻，则这样的排列方法有多少种（结果用数字表示）．（ ）
| A、5 | B、10 | C、20 | D、120 |
在直三棱柱ABC-A1B1C1中，若
=
，
=
，
=
，则
等于（ ）
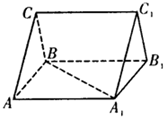
| CA |
| a |
| CB |
| b |
| CC1 |
| c |
| A1B |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|