Question

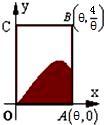
如图所示，矩形OABC内的阴影部分是由曲线f（x）=sinx（x∈（0，π））及直线x=θ（θ∈（0，π））与x轴围成，向矩形OABC内随机投掷一点，若落在阴影部分的概率为

3

8

，则θ的值是（　　）

• A、

  7π

  12

• B、

  2π

  3

• C、

  3π

  4

• D、

  5π

  6

Answer 1

考点：几何概型

专题：概率与统计

分析：由题意可得，是与面积有关的几何概率，分别求出构成试验的全部区域是矩形OABC的面积，构成事件A的区域即为阴影部分面积为∫

θ 0

sinxdx=-cosx|

θ 0

=1-cosa，代入几何概率的计算公式可求．

解答： 解：由题意可得，是与面积有关的几何概率
构成试验的全部区域是矩形OACB，面积为：θ×

4

θ

=4
记“向矩形OABC内随机投掷一点，若落在阴影部分”为事件A，
则构成事件A的区域即为阴影部分面积为∫₀^θsinxdx=-cosx|

θ 0

=1-cosθ
由几何概率的计算公式可得P（A）=

3

8

=

1-cosθ

4

，解得cosθ=-

1

2

，所以θ=

2π

3

；
故选：B．

点评：本题是与面积有关的几何概率的计算，求解需要分别计算矩形的面积及阴影部分的面积，考查了利用积分计算不规则图象的面积．