题目内容
用30cm长的铁丝围成一个扇形,应怎样设计才能使扇形的面积最大?最大面积是多少?
考点:扇形面积公式
专题:应用题
分析:设出扇形的圆心角α,半径r,面积S,弧长l,根据题意求出扇形面积S的表达式,求出最大值以及对应的半径r是多少.
解答:
解:设扇形的圆心角为α,半径为r,面积为S,弧长为l,
∴扇形的周长是l+2r=30;
∴l=30-2r,
∴S=
•l•r=
(30-2r)•r=-r2+15r=-(r-
)2+
;
∴当半径r=
cm时,
l=30-2×
=15cm,
∴扇形面积的最大值是
cm2,
这时α=
=2rad.
∴扇形的周长是l+2r=30;
∴l=30-2r,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| 225 |
| 4 |
∴当半径r=
| 15 |
| 2 |
l=30-2×
| 15 |
| 2 |
∴扇形面积的最大值是
| 225 |
| 4 |
这时α=
| l |
| r |
点评:本题考查了扇形面积的应用问题,解题时应建立目标函数,求目标函数的最值即可,是基础题.

练习册系列答案
相关题目
已知集合A={x|x≥4},g(x)=
的定义域为B,若A∩B=∅,则实数a的取值范围是( )
| 1 | ||
|
| A、(-2,4) |
| B、(3,+∞) |
| C、(-∞,3) |
| D、(-∞,3] |
已知函数f(x)=2x(-2≤x≤2),则函数y=f(2x)-2f(x)的最大值是( )
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、8 |
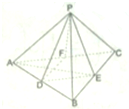 如图,在所有棱长都相等的正三棱锥P-ABC中,D,E,F分别是AB,BC,CA的中点,下列四个结论不成立的是( )
如图,在所有棱长都相等的正三棱锥P-ABC中,D,E,F分别是AB,BC,CA的中点,下列四个结论不成立的是( )| A、BC∥平面PDF |
| B、平面PDF⊥平面ABC |
| C、平面PAE⊥平面ABC |
| D、平面PDF⊥平面PAE |
函数f(x)=sin(
-2x),x∈R是( )
| 3π |
| 2 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|