题目内容
16.设Sn为数列{an}的前n项和,给出如下数列:①5,3,1,-1,-3,-5,-7,…;
②-14,-10,-6,-2,2,6,10,14,18,….
(1)对于数列①,计算S1,S2,S4,S5;对于数列②,计算S1,S3,S5,S7.
(2)根据上述结果,对于存在正整数k,满足ak+ak+1=0的这一类等差数列{an}前n项和的规律,猜想一个正确的结论,并加以证明.
分析 (1)直接求和,可得结论;
(2)ak+ak+1=0,2a1=(1-2k)d,证明S2k-n-Sn=0即可.
解答 解:(1)对于数列①S1=5,S2=8,S4=8,S5=5;②S1=-14,S3=-30,S5=-30,S7=-14;
(2)∵ak+ak+1=0,2a1=(1-2k)d
S2k-n-Sn=(2k-n)a1+$\frac{(2k-n)(2k-n-1)}{2}$d-na1-$\frac{n(n-1)}{2}d$
=$\frac{d}{2}$[(2k-n)(1-2k)+(2k-n)(2k-n-1)-(1-2k)n-n(n-1)]
=$\frac{d}{2}$[2k-4k2-n+2nk+4k2-2kn-2k-2nk+n2+n-n+2kn-n2+n]
=$\frac{d}{2}$•0=0
点评 本题考查数列求和,考查归纳推理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
5.定义运算a*b为执行如图所示的程序框图输出的S值,则${100^{(\frac{1}{2}lg9-lg2)}}*({log_9}8•{log_4}\root{3}{3})$的值为( )
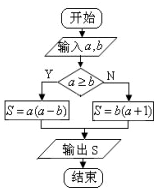

| A. | $\frac{13}{16}$ | B. | $\frac{9}{2}$ | C. | 4 | D. | 6 |
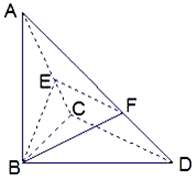 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}$=λ(0<λ<1).