题目内容
若
=
,则tanα的值为 .
| cos(π+α)•sin2(-α) |
| sin(π+α)•cos2(-α) |
| 1 |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简求解即可.
解答:
解:∵
=
,
∴
=
=tanα=
.
故答案为:
.
| cos(π+α)•sin2(-α) |
| sin(π+α)•cos2(-α) |
| 1 |
| 2 |
∴
| cos(π+α)•sin2(-α) |
| sin(π+α)•cos2(-α) |
=
| -cosα•sin2α |
| -sinα•cos2α |
=tanα=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查诱导公式的应用,三角函数的化简求值,基本知识的考查.

练习册系列答案
相关题目
已知正方形OABC的四个顶点分别是0(0,0),A(1,0),B(1,1),C(0,1)设u=x2-y2,v=2xy是一个由平面xOy到平面uOv上的变换,则正方形OABC在这个变换下的图形是( )
A、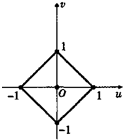 |
B、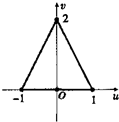 |
C、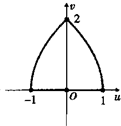 |
D、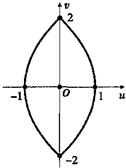 |
已知
=(1,2),
=(-2,-4),则
与
( )
| a |
| b |
| a |
| b |
| A、平行且反向 |
| B、平行且同向 |
| C、垂直 |
| D、既不平行也不垂直 |