题目内容
15.已知数列{an}前n项和为Sn,对任意p、q∈N*都有Sp+Sq=-p2-q2(1)求{an}的通项公式;
(2)令Cn=$\frac{1}{{{a}_{n}a}_{n+1}}$,求{an}前n项和Tn.
分析 (1)取p=q=n,可得Sn,然后结合$\left\{\begin{array}{l}{{a}_{1}={S}_{1}}\\{{a}_{n}={S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$求得{an}的通项公式;
(2)把{an}的通项公式代入Cn=$\frac{1}{{{a}_{n}a}_{n+1}}$,然后利用裂项相消法求{Cn}前n项和Tn.
解答 解:(1)∵p、q∈N*,令p=q=n,
∴Sn=-n2,
当n=1时,S1=a1=-1;
当n≥2时,an=Sn-Sn-1=-n2-[-(n-1)2]=-2n+1,
验证n=1时成立,
∴an=-2n+1;
(2)∵an=-2n+1,∴an+1=-2n-1,
∴Cn=$\frac{1}{{{a}_{n}a}_{n+1}}$=$\frac{1}{(-2n+1)(-2n-1)}=\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴Tn=C1+C2+C3+…+Cn=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$
=$\frac{1}{2}(1-\frac{1}{2n+1})=\frac{n}{2n+1}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了裂项相消法求数列的前n项和,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知函数$f(x)=sin({ωx-\frac{π}{6}})+\frac{1}{2}({ω>0})$,且$f(α)=-\frac{1}{2}$,$f(β)=\frac{1}{2}$,若|α-β|的最小值为$\frac{3π}{4}$,则ω的值为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
10.设点P是圆C:(x+4)2+(y-2)2=5上的动点,则点P到原点距离的最大值为( )
| A. | $\sqrt{5}$ | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | $4\sqrt{5}$ |
20.数列{an}的前项和为${S_n}({n∈{N^*}})$,且${a_1}=\frac{1}{2},{S_n}={n^2}{a_n}({n∈{N^*}})$,利用归纳推理,猜想{an}的通项公式为( )
| A. | ${a_n}=\frac{2n-4}{3^n}$ | B. | ${a_n}=\frac{1}{{n({n+1})}}({n∈{N^*}})$ | C. | ${a_n}=\frac{1}{2n}$ | D. | ${a_n}=\frac{2}{n}$ |
5.某算法的程序框图如图所示,若输出的y=$\frac{{\sqrt{2}}}{2}$,则输入的x的值可能为( )


| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
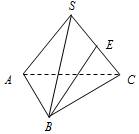 如图,三棱锥S-ABC中,若$AC=2\sqrt{3}$,SA=SB=SC=AB=BC=4,E为棱SC的中点,则直线AC与BE所成角的余弦值为$\frac{1}{4}$,直线AC与平面SAB所成的角为600.
如图,三棱锥S-ABC中,若$AC=2\sqrt{3}$,SA=SB=SC=AB=BC=4,E为棱SC的中点,则直线AC与BE所成角的余弦值为$\frac{1}{4}$,直线AC与平面SAB所成的角为600.