题目内容
7.有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.(1)排成前后两排,前排3人.后排4人
(2)全体站成一排,甲不站排头也不站排尾;
(3)全体站成一排,女生必须站在一起;
(4)全体站成一排,男生互不相邻.
分析 (1)根据题意,将7人全排列即可,由排列数公式计算可得答案;
(2)根据题意,分2步进行分析:先分析甲,再将其余6人全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(3)根据题意,用插空法分2步进行分析:先将女生看成一个整体,考虑女生之间的顺序,再将女生的整体与3名男生在一起进行全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(4)根据题意,用插空法分析:先将4名女生全排列,再在女生之间及首尾空出的5个空位中任选3个空位排男生,分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:(1)根据题意,将7人全排列即可,则共有A77种=5 040种方法.
(2)根据题意,分2步进行分析:
先排甲,由于甲不站排头也不站排尾,则甲有5种方法,
其余6人全排列,安排在其他位置,有A66种方法,
故共有5×A66=3 600种方法.
(3)根据题意,分2步进行分析:
将女生看成一个整体,考虑女生之间的顺序,有A44种情况,
再将女生的整体与3名男生在一起进行全排列,有A44种情况,
故共有A44A44=576种方法.
(4)根据题意,分2步进行分析:
先排女生,将4名女生全排列,有A44种方法,
再安排男生,由于男生不相邻,可以在女生之间及首尾空出的5个空位中任选3个空位排男生,有A53种方法,
故共有A44×A53=1440种方法.
点评 本题考查排列、组合的综合应用,涉及分步、分类计数原理的应用,需要掌握特殊问题的处理方法.

练习册系列答案
相关题目
3.假设你家订了一份牛奶,送奶人在早上6:30~7:30之间随机地把牛奶送到你家,而你在早上7:00~8:00之间随机离家上学,则你在离家前能收到牛奶的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
18.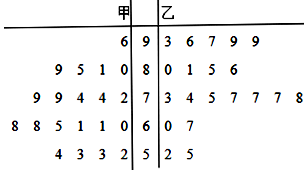 为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
(1)分别计算甲、乙两班20个样本中,数学分数前十的平均分;
(2)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$.(n=a+b+c+d)
独立性检验临界表
 为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.
为推行“新课堂”教学法,某数学老师分别用原传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图.记成绩不低于70分者为“成绩优良”.(1)分别计算甲、乙两班20个样本中,数学分数前十的平均分;
(2)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
独立性检验临界表
| P(K2≥0) | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 |
16.已知圆x2+y2+2x-6y+5=0,将直线y=2x+λ向上平移2个单位与之相切,则实数λ的值为( )
| A. | -7或3 | B. | -2或8 | C. | -4或4 | D. | 0或6 |