题目内容
已知二次函数y=n(n+1)x2-(2n+1)x+1,当n依次取1,2,3,4,…,k时,其图象在x轴上截得的线段长度的总和为
- A.1
- B.

- C.
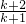
- D.
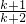
B
分析:先求出二次函数的零点即得图象在x轴上截得的线段长度,进而利用裂项求和即可得出答案.
解答:由n(n+1)x2-(2n+1)x+1=0,解得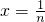 或
或 ,
,
∴二次函数y=n(n+1)x2-(2n+1)x+1,当n依次取1,2,3,4,…,k时,其图象在x轴上截得的线段长度总和=(1-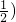
 +…+
+…+ =
= =
= .
.
故选B.
点评:熟练掌握二次函数的性质和裂项求和是解题的关键.
分析:先求出二次函数的零点即得图象在x轴上截得的线段长度,进而利用裂项求和即可得出答案.
解答:由n(n+1)x2-(2n+1)x+1=0,解得
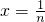 或
或 ,
,∴二次函数y=n(n+1)x2-(2n+1)x+1,当n依次取1,2,3,4,…,k时,其图象在x轴上截得的线段长度总和=(1-
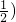
 +…+
+…+ =
= =
= .
.故选B.
点评:熟练掌握二次函数的性质和裂项求和是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目


