题目内容
15.某电子广告牌连续播出四个广告,假设每个广告所需的时间互相独立,且都是整数分钟,经统计,以往播出100次所需的时间(t)的情况如下:| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
(Ⅰ)求恰好在第6分钟后开始播出第3号广告的概率;
(Ⅱ)用X表示至第4分钟末已完整播出广告的次数,求x的分布列及数学期望.
分析 (Ⅰ)恰好在第6分钟后开始播出第3号广告包含四种情况:①1号广告连播3次,然后播第3号广告;②2号广告连播2次,然后播第3号广告;③1号广告和3号广告播完后,播第3号广告;④4号广告播完后,播第3号广告.由此能求出恰好在第6分钟后开始播出第3号广告的概率.
(II)由已知得X的可能取值为0,1,2,分别求出相应的概率,由此能求出x的分布列及数学期望.
解答 解:(Ⅰ)设事件A表示“播1号广告”,事件B表示“播2号广告”,事件C表示“播3号广告”,事件D表示“播4号广告”,
由条件知P(A)=$\frac{20}{100}$=$\frac{2}{10}$,P(B)=$\frac{300}{100}=\frac{3}{10}$,P(C)=$\frac{40}{100}$=$\frac{4}{10}$,P(B)=$\frac{10}{100}$=$\frac{1}{10}$,
恰好在第6分钟后开始播出第3号广告包含四种情况:
①1号广告连播3次,然后播第3号广告;②2号广告连播2次,然后播第3号广告;
③1号广告和3号广告播完后,播第3号广告;④4号广告播完后,播第3号广告,
∴恰好在第6分钟后开始播出第3号广告的概率:
p=$(\frac{2}{10})^{3}$×$\frac{4}{10}$+$(\frac{3}{10})^{2}×\frac{4}{10}$+${C}_{2}^{1}×\frac{2}{10}×\frac{4}{10}×\frac{4}{10}$+$\frac{1}{10}×\frac{4}{10}$=$\frac{179}{1250}$.
(II)由已知得X的可能取值为0,1,2,
P(X=0)=$\frac{1}{10}$,
P(X=1)=$\frac{4}{10}+{C}_{2}^{1}•\frac{2}{10}•\frac{3}{10}$+$\frac{2}{10}•\frac{4}{10}$+$\frac{3}{10}•\frac{4}{10}$+$\frac{2}{10}•\frac{1}{10}+\frac{3}{10}•\frac{1}{10}$+$\frac{3}{10}•\frac{3}{10}$=$\frac{86}{100}$,
P(X=2)=$\frac{2}{10}•\frac{2}{10}$=$\frac{4}{100}$,
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{86}{100}$ | $\frac{4}{100}$ |
点评 本题考查概率的求法,考查离散随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案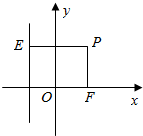 如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).
如图,点O是坐标原点,点F(p,0),其中p>0,点E在直线l:x=-p上,点F到直线x+y=0的距离等于$\sqrt{2}$,动点p满足|$\overrightarrow{PE}$|=|$\overrightarrow{FP}$|,$\overrightarrow{EP}$=λ$\overrightarrow{OF}$(λ∈R,且λ≠0).