题目内容
设向量a＝(2，sin θ)，b＝(1，cos θ)，θ为锐角．
(1)若a·b＝
，求sin θ＋cos θ的值；
(2)若a∥b，求sin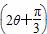
的值．
解 (1)因为a·b＝2＋sin θcos θ＝，
所以sin θcos θ＝
.(2分)
所以(sin θ＋cos θ)2＝1＋2sin θcos θ＝
.
又因为θ为锐角，所以sin θ＋cos θ＝
.(5分)
(2)法一 因为a∥b，所以tan θ＝2.(7分)
所以sin 2θ＝2sin θcos θ＝
＝
，
cos 2θ＝cos2θ－sin2θ＝
＝－
.(11分)
法二 因为a∥b，所以tan θ＝2.(7分)
所以sin θ＝
，cos θ＝
.
因此sin 2θ＝2sin θcos θ＝，
cos 2θ＝cos2θ－sin2θ
＝－.(11分)
练习册系列答案
相关题目
，则该三棱锥的左视图的面积为
D.
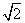acos B＝ccos B＋bcos C.
(S2n＋S2m)－(
n－m)2，其中m，n为任意正整数．
－
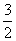an＋33＝k2的所有正整数k，n.
中，已知
且
．
的值；
，求边AC的长．