题目内容
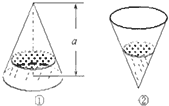 如图①,一个圆锥形容器的高为a=2,内装有高度为h的一定量的水,如果将容器倒置,这时水所形成的圆锥的高恰为1(如图②),则图①中的水面高度h=
如图①,一个圆锥形容器的高为a=2,内装有高度为h的一定量的水,如果将容器倒置,这时水所形成的圆锥的高恰为1(如图②),则图①中的水面高度h=考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:圆锥正置与倒置时,水的体积不变,另外水面是平行于底面的平面,此平面截得的小圆锥与原圆锥成相似体,它们的体积之比为对应高的立方比.
解答:
解:令圆锥倒置时水的体积为V′,圆锥体积为V,
则
=13÷23=
,
∴
=
,
倒置后:V水=
V,
设此时水高为h,则
h3:23=7:8,
∴h=
,
故原来水面的高度为2-
,
故答案为:2-
则
| V′ |
| V |
| 1 |
| 8 |
∴
| V空 |
| V锥 |
| 7 |
| 8 |
倒置后:V水=
| 1 |
| 8 |
设此时水高为h,则
h3:23=7:8,
∴h=
| 3 | 7 |
故原来水面的高度为2-
| 3 | 7 |
故答案为:2-
| 3 | 7 |
点评:此题若用V水=V台计算是比较麻烦的,因为台体的上底面半径还需用h1=
h导出来,我们用V水=V锥-V空,而V空与V锥的体积之间有比例关系,可以直接求出.
| 1 |
| 3 |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
下列函数中,既是奇函数又是增函数的为( )
| A、y=cosx-1 | ||
| B、y=-x2 | ||
| C、y=x•|x| | ||
D、y=-
|
在实数集上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+a)<1对任意实数x都成立,则实数a的取值范围是( )
A、(-
| ||||
| B、(0,2) | ||||
| C、(-1,1) | ||||
D、(-
|
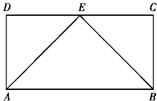 如图,矩形ABCD中,点E为边CD的中点,若在矩形中随机撒一粒黄豆,则黄豆落在△ABE内的概率为
如图,矩形ABCD中,点E为边CD的中点,若在矩形中随机撒一粒黄豆,则黄豆落在△ABE内的概率为


