题目内容
设实数x，y满足3x2+2y2≤6，则P=2x+y的最大值为（ ）
| A、11 | ||
B、
| ||
| C、6 | ||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设x=
cosα，y=
sinα，则P=2x+y=2
cosα+
sinα=
sin（α+θ），即可求出P=2x+y的最大值．
| 2 |
| 3 |
| 2 |
| 3 |
| 11 |
解答：
解：设x=
cosα，y=
sinα，
则P=2x+y=2
cosα+
sinα=
sin（α+θ），
∴P=2x+y的最大值为
．
故选：B．
| 2 |
| 3 |
则P=2x+y=2
| 2 |
| 3 |
| 11 |
∴P=2x+y的最大值为
| 11 |
故选：B．
点评：本题考查椭圆的简单性质，考查椭圆的参数方程，比较基础．
练习册系列答案
相关题目
双曲线的焦点为（0，6），（0，-6），且经过点A（-5，6），则其标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若P（x，y）在直线x+y-4=0上，则x2+y2的最小值是（ ）
| A、8 | ||
B、2
| ||
C、
| ||
| D、16 |
曲线y=3xlnx+x在点（1，1）处的切线与坐标轴所围三角形的面积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、9 |
在程序框图中处理框的功能表示（ ）
| A、输入信息 |
| B、输出信息 |
| C、赋值，计算 |
| D、一个算法的起始和结束 |
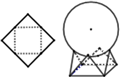如图，用一边长为| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f（x）=
，若a，b，c互不相等，且f（a）=f（b）=f（c），则a+b+c的取值范围为（ ）
|
A、（
| ||||
B、（
| ||||
C、（
| ||||
| D、（6，l2） |
如图所示的四棱锥P-ABCD的底面ABCD是边长为a（a＞0）的菱形，∠ABC=60°，点P在底面的射影O在DA的延长线上，且OC过边AB的中点E．