题目内容
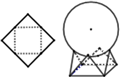 如图,用一边长为
如图,用一边长为| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:球的体积和表面积
专题:
分析:蛋槽的边长是原来硬纸板的对角线长度的一半,为1cm,蛋槽立起来的小三角形部分高度是
,鸡蛋的半径根据已知的表面积4π=4πr2得到r=1cm,直径D=2cm,大于折好的蛋巢边长1cm,由此能求出鸡蛋中心(球心)与蛋巢底面的距离.
| 1 |
| 2 |
解答:
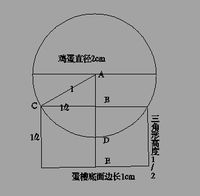 解:蛋槽的边长是原来硬纸板的对角线长度的一半,为1cm,
解:蛋槽的边长是原来硬纸板的对角线长度的一半,为1cm,
蛋槽立起来的小三角形部分高度是
,
鸡蛋的半径根据已知的表面积4π=4πr2得到r=1cm,直径D=2cm,大于折好的蛋巢边长1cm,
四个三角形的顶点所在的平面在鸡蛋表面所截取的小圆直径就是蛋槽的边长1cm,
根据图示,AB段由三角形AB求出得:AB=
,
AE=AB+BE=
+
,
∴鸡蛋中心(球心)与蛋巢底面的距离为
+
.
故选:D.
 解:蛋槽的边长是原来硬纸板的对角线长度的一半,为1cm,
解:蛋槽的边长是原来硬纸板的对角线长度的一半,为1cm,蛋槽立起来的小三角形部分高度是
| 1 |
| 2 |
鸡蛋的半径根据已知的表面积4π=4πr2得到r=1cm,直径D=2cm,大于折好的蛋巢边长1cm,
四个三角形的顶点所在的平面在鸡蛋表面所截取的小圆直径就是蛋槽的边长1cm,
根据图示,AB段由三角形AB求出得:AB=
| ||
| 2 |
AE=AB+BE=
| ||
| 2 |
| 1 |
| 2 |
∴鸡蛋中心(球心)与蛋巢底面的距离为
| ||
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查点、线、面间距离的计算,解题时要认真审题,注意挖掘题设中的隐含条件,合理地化空间问题为平面问题,注意数形结合法的合理运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
10件产品中有5件次品,从中不放回的抽取2次,每次抽1件,已知第一次抽出的是次品,则第二次抽出的是正品的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
p:7是质数,q:8是12的约数,则命题“p∨q”,“p∧q”的真假是( )
| A、真,真 | B、真,假 |
| C、假,真 | D、假,假 |
对空间任意两个向量
,
(
≠0),
∥
的充要条件是( )
| a |
| b |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设实数x,y满足3x2+2y2≤6,则P=2x+y的最大值为( )
| A、11 | ||
B、
| ||
| C、6 | ||
D、
|
设双曲线
-
=1上一点P,F1,F2是焦点,若|PF1|=10,则|PF2|等于( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、2 | B、2或18 | C、18 | D、16 |
直线l1∥l2,l1上有4个点,l2上有6个点,以这些点为端点连成线段,他们在l1与l2之间最多的交点个数是( )
| A、24 | B、45 | C、80 | D、90 |