题目内容
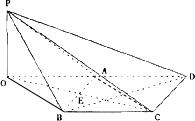
 如图所示的四棱锥P-ABCD的底面ABCD是边长为a(a>0)的菱形,∠ABC=60°,点P在底面的射影O在DA的延长线上,且OC过边AB的中点E.
如图所示的四棱锥P-ABCD的底面ABCD是边长为a(a>0)的菱形,∠ABC=60°,点P在底面的射影O在DA的延长线上,且OC过边AB的中点E.(1)证明:BD⊥平面POB;
(2)若PO=
| a |
| 2 |
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)证明四边形OACB是边长为a(a>0)的菱形,可得OB⊥BD,PO⊥底面ABCD,可得PO⊥BD,即可证明BD⊥平面POB;
(2)由等体积VO-PAC=VP-OAC,求三棱锥O-PAC的体积.
(2)由等体积VO-PAC=VP-OAC,求三棱锥O-PAC的体积.
解答:
 (1)证明:连接AC,
(1)证明:连接AC,
∵四棱锥P-ABCD的底面ABCD是边长为a(a>0)的菱形,∠ABC=60°,
∴AC=a,
∵边AB的中点E,
∴OC⊥AB,
∵AB∥CD,
∴OC⊥CD,AE∥CD,AE=
CD,
∵∠ADC=60°,
∴A,E分别为OD,OC的中点,
连接OB,则四边形OACB是边长为a(a>0)的菱形,
连接BD,在菱形ABCD中,AC⊥BD,∴OB⊥BD,
∵PO⊥底面ABCD,
∴PO⊥BD,
∵PO∩BO=O,
∴BD⊥平面POB;
(2)解:由等体积VO-PAC=VP-OAC,OC=
,AE=
AB=
,
∴VO-PAC=VP-OAC=
×
×OC×AE×PO=
×
a×
×
=
.
∴三棱锥O-PAC的体积为
.
 (1)证明:连接AC,
(1)证明:连接AC,∵四棱锥P-ABCD的底面ABCD是边长为a(a>0)的菱形,∠ABC=60°,
∴AC=a,
∵边AB的中点E,
∴OC⊥AB,
∵AB∥CD,
∴OC⊥CD,AE∥CD,AE=
| 1 |
| 2 |
∵∠ADC=60°,
∴A,E分别为OD,OC的中点,
连接OB,则四边形OACB是边长为a(a>0)的菱形,
连接BD,在菱形ABCD中,AC⊥BD,∴OB⊥BD,
∵PO⊥底面ABCD,
∴PO⊥BD,
∵PO∩BO=O,
∴BD⊥平面POB;
(2)解:由等体积VO-PAC=VP-OAC,OC=
| 3 |
| 1 |
| 2 |
| a |
| 2 |
∴VO-PAC=VP-OAC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| a |
| 2 |
| a |
| 2 |
| ||
| 24 |
∴三棱锥O-PAC的体积为
| ||
| 24 |
点评:本小题主要考查直线与平面垂直的判定,以及三棱锥体积的计算等有关知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于中档题.

练习册系列答案
相关题目
实验中学采取分层抽样的方法从应届高一学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示
根据表中数据,利用公式计算x2=
的值,若断定实验中学的高一学生选报文理科与性别有关,那么这种判断出错的可能性为( )
| 男 | 女 | |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
| n×(ad-bc)2 |
| (a+d)(b+c)(a+c)(b+d) |
| A、0.1 | B、0.05 |
| C、0.01 | D、0.001 |
设实数x,y满足3x2+2y2≤6,则P=2x+y的最大值为( )
| A、11 | ||
B、
| ||
| C、6 | ||
D、
|
直线l1∥l2,l1上有4个点,l2上有6个点,以这些点为端点连成线段,他们在l1与l2之间最多的交点个数是( )
| A、24 | B、45 | C、80 | D、90 |