题目内容
函数f(x)=ln(e-x2)的图象是( )
A、 |
B、 |
C、 |
D、 |
考点:函数的图象,复合函数的单调性
专题:函数的性质及应用
分析:根据函数的对称性和奇偶性以及函数的取值即可得到结论.
解答:
解:由e-x2>0,得-
<x<
,则f(x)为偶函数关于y轴对称,
f(0)=lne=1,排除B,D,
当0<x<1时,函数t=e-x2为减函数,而y=lnt为增函数,根据复合函数单调性的性质可知此时函数f(x)为减函数,故排除C,
故选:A
| e |
| e |
f(0)=lne=1,排除B,D,
当0<x<1时,函数t=e-x2为减函数,而y=lnt为增函数,根据复合函数单调性的性质可知此时函数f(x)为减函数,故排除C,
故选:A
点评:本题主要考查函数图象的识别和判断,根据函数的取值性质以及复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
在同一直角坐标系中,函数f(x)=logax(a>0,a≠1)与函数g(x)=ax(a>0,a≠1)的图象可能是( )
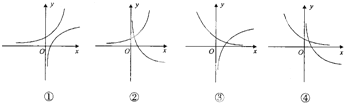

| A、①② | B、①③ | C、①④ | D、②④ |
在△ABC中,若AB=
,C=150°,则它的外接圆的面积为( )
| 3 |
| A、π | B、2π | C、3π | D、4π |
函数f(x)=
的定义域为( )
| 2x-1 |
| log3x |
| A、(0,+∞) |
| B、(1,+∞) |
| C、(0,1) |
| D、(0,1)∪(1,+∞) |
计算:
=( )
| 2i |
| i-1 |
| A、i+1 | B、i-1 |
| C、-i+1 | D、-i-1 |