题目内容
17．已知复数z=m2（1+i）-m（m+i）（m∈R），若z是实数，则m的值为0或1．分析 利用复数的运算法则、复数为实数的充要条件即可得出．
解答 解：复数z=m2（1+i）-m（m+i）=（m2-m）i（m∈R）是实数，
∴m2-m=0，解得m=0或1．
故答案为：0或1．
点评 本题考查了复数的运算法则、复数为实数的充要条件，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
7．在直角△ABC中，∠BCA=90°，CA=CB=1，P为AB边上的点$\overrightarrow{AP}$=λ$\overrightarrow{AB}$，若$\overrightarrow{CP}•\overrightarrow{AB}≥\overrightarrow{PA}•\overrightarrow{PB}$，则λ的最小值是（ ）
| A． | 1 | B． | $\frac{{2-\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\sqrt{2}$ |
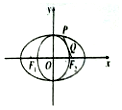如图，F1，F2是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右两焦点，点P在椭圆C上，线段PF2与圆x2+y2=b2相切于点Q，且点Q是线段PF2的中点，则${\frac{{{a^2}+{e^2}}}{3b}^{\;}}$（e为椭圆的离心率）的最小值为$\frac{\sqrt{5}}{3}$．
如图，已知菱形ABCD与直角梯形ABEF所在的平面互相垂直，其中BE∥AF，AB⊥AF，AB=BE=$\frac{1}{2}$AF=2，∠CBA=$\frac{π}{3}$，P为DF的中点．