题目内容
设F1、F2分别是椭圆 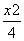 +y2=1的左、右焦点.
+y2=1的左、右焦点.
(Ⅰ)若P是第一象限内该椭圆上的一点,且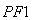 ·
·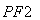 =-
=-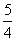 ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且点O在以AB为直径的圆的外部(其中O为坐标原点),求直线l的斜率k的取值范围.
解:)易知 ,
, ,
, .
.
∴ ,
, .设
.设
 .则
.则
 ,又
,又 ,
,
联立 ,解得
,解得 ,
, .……………5分
.……………5分
(Ⅱ)显然 不满足题设条件.可设
不满足题设条件.可设 的方程为
的方程为 ,设
,设 ,
, .
.
联立
∴ ,
,
由
 ,
, ,得
,得 .①
.①
又 为锐角
为锐角 ,
,
∴
又
∴




∴ .②
.②
综①②可知 ,∴
,∴ 的取值范围是
的取值范围是 .……13分
.……13分

练习册系列答案
相关题目
 的首项为2,公差为
的首项为2,公差为 ,其前
,其前 项和
项和 满足:对于任意的
满足:对于任意的 ,都有
,都有 是非零常数.则
是非零常数.则 .
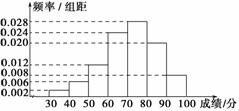
.
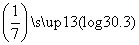 ,比较a, b, c的大小
,比较a, b, c的大小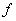 (x)=23x-1+1过定点A,且点A在直线l:3mx+ny=4(m>0,n>0)上,则
(x)=23x-1+1过定点A,且点A在直线l:3mx+ny=4(m>0,n>0)上,则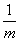 +
+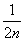 的取值范围是____________.
的取值范围是____________.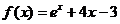 的零点所在区间为 ( )
的零点所在区间为 ( )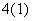 ,0) B.(0,
,0) B.(0, ) D.(
) D.(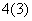 )
) 在曲线
在曲线 上,
上,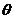 为该曲线在点
为该曲线在点 ,且
,且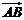 与
与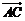 满足
满足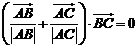 ,
,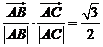 ,则
,则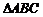 的面积为( ).
的面积为( ). B.
B. C.
C.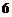 D.
D.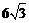
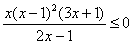 的解集是_________________.
的解集是_________________.