题目内容
19.设随机变量X~N(2,1),则P(|X|<1)=( )附:(若随机变量ξ~N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%,P(μ-3σ<ξ<μ+3σ)=99.72%)
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
分析 由题意,P(1<X<3)=0.6826,P(-1<X<5)=0.9972,利用P(|X|<1)=$\frac{1}{2}$[P(-1<X<5)-P(1<X<3)],可得结论.
解答 解:由题意,P(1<X<3)=0.6826,P(-1<X<5)=0.9972,
∴P(|X|<1)=$\frac{1}{2}$[P(-1<X<5)-P(1<X<3)]=0.1573,
故选B.
点评 本题考查概率的计算,考查正态分布曲线的对称性,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知函数$f(x)=\sqrt{3}sin2x-cos2x$的图象在区间$[{0,\frac{a}{3}}]$和$[{2a,\frac{4π}{3}}]$上均单调递增,则正数a的取值范围是( )
| A. | $[{\frac{π}{6},\frac{5π}{12}}]$ | B. | $[{\frac{5π}{12},π}]$ | C. | $[{\frac{π}{4},π}]$ | D. | $[{\frac{π}{4},\frac{2π}{3}}]$ |
4.已知$\overrightarrow a=({sin\frac{ω}{2}x,sinωx}),\overrightarrow b=({sin\frac{ω}{2}x,\frac{1}{2}})$,其中ω>0,若函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$在区间(π,2π)内没有零点,则ω的取值范围是( )
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |
11.已知集合M={x|1<x≤3},若N={x|2<x≤5},则M∪N=( )
| A. | {x|1<x≤5} | B. | {x|2<x≤3} | C. | {x|1≤x<2或3≤x≤5}} | D. | {x|1≤x≤5} |
8. 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
9.某超市计划每天购进某商品若干件,该超市每销售一件该商品可获利润80元,若供大于求,剩余商品全部退回,但每件商品亏损20元;若供不应求,则从外部调剂,此时每件调剂商品可获利40元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量n(单位:件,n∈N),整理得下表:
若商店一天购进10件该商品,以50天记录的各需求量的频率作为各需求量发生的概率,求当天的利润在区间[800,900]内的概率.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量n(单位:件,n∈N),整理得下表:
| 日需求量 | 7 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 5 | 7 | 10 | 14 | 10 | 4 |
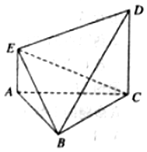 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.