题目内容
已知桉树f(x)为定义在R上的奇函数,当x>0是,都有f(x+
)•f(x)=4,且当x∈(0,
]时,f(x)=2x+1,则f(-2012)+f(2013)= .
| 3 |
| 2 |
| 3 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据根据已知条件能够求得f(x)=4[f(x-
n)](-1)n,从而便可求出f(2012)=2,f(2013)=0,所以f(-2012)+f(2013)=-f(2012)+f(2013)=-2.
| 3 |
| 2 |
解答:
解:根据已知条件,f(x)=4[f(x-
n)](-1)n;
∴f(2012)=4[f(2012-
•1341)]-1=
=
=2;
f(2013)=4[f(2013-
•1342)]1=4f(0)=0;
∴f(-2012)+f(2013)=-2+0=-2.
故答案为:-2.
| 3 |
| 2 |
∴f(2012)=4[f(2012-
| 3 |
| 2 |
| 4 | ||
f(
|
| 4 |
| 2 |
f(2013)=4[f(2013-
| 3 |
| 2 |
∴f(-2012)+f(2013)=-2+0=-2.
故答案为:-2.
点评:考查奇函数的定义,奇函数在原点有定义时,f(0)=0,以及根据已知条件将2012,2013变化到区间(0,
]上的方法.
| 3 |
| 2 |

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
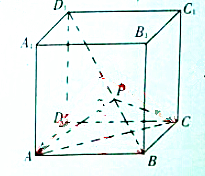
如图,已知正方体ABCD-A1B1C1D1棱长为1,点P在线段BD1上,当∠APC最大时,三棱锥P-ABC的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
当0<x<y<
时,给出以下结论(其中e是自然对数的底数):①excosy<eycosx,②excosy>eycosx,③excosx<eycosy,④excosx>eycosy,其中正确结论的序号是( )
| π |
| 4 |
| A、①③ | B、①④ | C、②③ | D、②④ |
已知函数f(x)是定义在R上的函数且满足f(x+
)=-f(x),若x∈(0,3)时,f(x)=log2(3x+1),则f(2011)=( )
| 3 |
| 2 |
| A、4 |
| B、-2 |
| C、2 |
| D、log27 |