题目内容
14.某次军事演习要出动一艘航母,2艘攻击型潜艇一前一后,3艘驱逐舰和3艘护卫舰分列左右,每侧3艘,同侧不能都是同种舰艇,则舰艇分配方案的方法数为( )| A. | 72 | B. | 324 | C. | 648 | D. | 1296 |
分析 利用间接法,先分步,先求出核潜艇排列数为A22,再求出6艘舰艇任意排列的排列数为A66,同侧均是同种舰艇的排列数为A33A33×2,问题得以解决.
解答 解:核潜艇排列数为A22,6艘舰艇任意排列的排列数为A66,同侧均是同种舰艇的排列数为A33A33×2,则舰艇分配方案的方法数为A22(A66-A33A33×2)=1296.
故选:D.
点评 本题考查排列组合知识,考查学生分析解决问题的能力,正确运用乘法原理是关键.

练习册系列答案
相关题目
9.已知点M是△ABC所在平面内的一点,且满足5$\overrightarrow{AM}$=$\overrightarrow{AB}$+2$\overrightarrow{AC}$,则△AMB与△ABC的面积比为( )
| A. | $\frac{5}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{5}{7}$ |
19.用反证法证明某命题时,对其结论:“自然数a、b、c中恰有一个奇数”正确的反设为( )
| A. | a、b、c都是奇数 | |
| B. | a、b、c都是偶数 | |
| C. | a、b、c中至少有两个奇数 | |
| D. | a、b、c中至少有两个奇数或都是偶数 |
3.等差数列{an}的首项a1=-5,它的前11项的平均值为5,若从中抽去一项,余下的10项的平均值为4.6,则抽去的是( )
| A. | a6 | B. | a8 | C. | a9 | D. | a10 |
4.已知命题p:?x∈R,cosx>sinx,命题q:?x∈(0,π),sinx+$\frac{1}{sinx}$>2,则下列判断正确的是( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
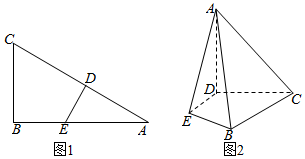 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).