题目内容
若A
>6C
,则正整数n的取值集合为 .
2 n |
4 n |
考点:组合及组合数公式,排列及排列数公式
专题:不等式的解法及应用,排列组合
分析:根据排列与组合公式,把不等式A
>6C
化为n(n-1)>6•
,
整理并解出该不等式,求出正整数n的取值集合即可.
2 n |
4 n |
| n(n-1)(n-2)(n-3) |
| 1×2×3×4 |
整理并解出该不等式,求出正整数n的取值集合即可.
解答:
解:∵A
>6C
,
∴n(n-1)>6•
,
即4>(n-2)(n-3),
整理得n2-5n+2<0,
解得
<n<
;
又∵0<
<
,4<
<5;
∴正整数n的取值集合为{1,2,3,4}.
故答案为:{1,2,3,4}.
2 n |
4 n |
∴n(n-1)>6•
| n(n-1)(n-2)(n-3) |
| 1×2×3×4 |
即4>(n-2)(n-3),
整理得n2-5n+2<0,
解得
5-
| ||
| 2 |
5+
| ||
| 2 |
又∵0<
5-
| ||
| 2 |
| 1 |
| 2 |
5+
| ||
| 2 |
∴正整数n的取值集合为{1,2,3,4}.
故答案为:{1,2,3,4}.
点评:本题考查了排列与组合数公式的应用问题,也考查了解不等式的应用问题,是基础题目.

练习册系列答案
相关题目
若某几何体的三视图如图所示,则此几何体的体积等于( )
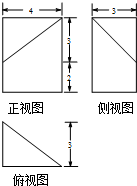

| A、4 | B、12 | C、24 | D、30 |
已知点A(0,0)、B(2,1)、C(5,5),则向量
在
方向上的投影为( )
| AB |
| AC |
A、
| ||||
B、3
| ||||
C、
| ||||
D、
|
| ∫ |
0 |
| cos2x |
| cosx+sinx |
A、2(
| ||
B、
| ||
C、
| ||
D、2-
|