题目内容

19．在△ABC中，若a=9，b=10，c=12，则△ABC的形状是（　　）
A．锐角三角形B．直角三角形
C．最大角为120°的钝角三角形D．最大角小于120°的钝角三角形

分析 利用余弦定理求出最大角的余弦值判断．

解答 解：∵a＜b＜c，∴A＜B＜C．
cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{81+100-144}{180}$=$\frac{37}{180}$＞0，∴C＜90°，∴△ABC是锐角三角形．
故选：A．

点评 本题考查了余弦定理得应用，属于基础题．

练习册系列答案
相关题目
9．已知函数f（x）满足f（$\frac{x}{2}$）=x+$\frac{1}{x}$．
（1）求函数的解析式；
（2）判断函数f（x）在区间（$\frac{1}{2}$，+∞）上的单调性，并用定义法加以证明．
10．若30°≤θ＜90°或90°＜θ＜120°，试确定tanθ的取值范围．
7．设x5=a0+a1（x-1）+a2（x-1）2+…+a5（x-1）5，那么a1+a2+…+a5=31．
14．在△ABC中，已知角A，B，C的对边分别为a，b，c，bc=60$\sqrt{3}$，sinA=sinB，面积S=15$\sqrt{3}$，求a的值．
4．若四边形ABCD中，$\overrightarrow{AB}$=$\overrightarrow{DC}$，|$\overrightarrow{AB}$+$\overrightarrow{BC}$|=|$\overrightarrow{AB}$-$\overrightarrow{BC}$|．求证：四边形ABCD是矩形．
11．已知$\overrightarrow{a}$=（2cosx，1），$\overrightarrow{b}$=（sinx-cosx，1），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，x∈R．
（1）求函数f（x）图象的对称中心坐标；
（2）求函数f（x）在区间[$\frac{π}{8}$，$\frac{3π}{4}$]上的最小值和最大值．
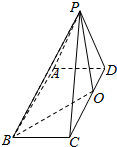15．已知点P为矩形ABCD所在平面外一点，AB=3，BC=2，平面PAB∩平面PCD=l．
（1）求证：l⊥AD；
（2）若点P在平面ABCD上的射影0在线段CD上，满足CO=20D，且直线PB与平面ABCD所成角的正切值为$\frac{1}{2}$，求四棱锥P-DABO的体积．
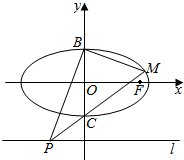16．如图，已知椭圆O：$\frac{{x}^{2}}{4}$+y2=1的右焦点为F，点B，C分别是椭圆O的上、下顶点，点P是直线l：y=-2上的一个动点（与y轴交点除外），直线PC交椭圆于另一点M．
（1）当直线PM过椭圆的右焦点F时，求△FBM的面积；
（2）①记直线BM，BP的斜率分别为k1，k2，求证：k1•k2为定值；
②求$\overrightarrow{PB}$•$\overrightarrow{PM}$的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网