题目内容
6.直角三角形的直角顶点在坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,且一直角边的方程是y=2x,斜边长是5,求此抛物线的方程.分析 将直线方程与抛物线方程联立,求得交点坐标,再利用斜边长为5,即可求得抛物线的方程.
解答 解:因为一直角边的方程是y=2x,所以另一直角边的方程是y=-$\frac{1}{2}$x.
由$\left\{\begin{array}{l}{y=2x}\\{{y}^{2}=2px}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{p}{2}}\\{y=p}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍去);
由$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{{y}^{2}=2px}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=8p}\\{y=-4p}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍去),
∴三角形的另两个顶点为($\frac{p}{2}$,p)和(8p,-4p).
∴$\sqrt{(\frac{p}{2}-8p)^{2}+(p+4p)^{2}}$=5解得p=$\frac{2\sqrt{13}}{13}$,
故所求抛物线的方程为2=$\frac{4\sqrt{13}}{13}$x.
点评 本题考查抛物线的标准方程,解题的关键是将直线方程与抛物线方程联立,求得交点坐标,属于中档题.

练习册系列答案
相关题目
5.直线y=kx-2交抛物线y2=8x于A、B两点,若AB中点横坐标为2,则|AB|为( )
| A. | $\sqrt{15}$ | B. | $2\sqrt{15}$ | C. | $\sqrt{42}$ | D. | $3\sqrt{15}$ |
2.椭圆$\frac{x^2}{3}+\frac{y^2}{5}=1$的焦距是( )
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
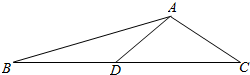 在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD
在△ABC中,∠BAD=30°,AB=4,AC=2,点D在BC上,且BC=2BD