题目内容
设{an}为公比q＞1的等比数列，若a2006和a2007是方程4x2-8x+3=0的两根，则a2008+a2009= ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：先利用一元二次方程的根与系数的关系得到以a2006+a2007=2，a2006•a2007=
；再把所得结论用a2006和q表示出来，求出q；最后把所求问题也用a2006和q表示出来即可的出结论．
| 3 |
| 4 |
解答：
解：设等比数列的公比为q．
∵a2006和a2007是方程4x2-8x+3=0的两个根
∴a2006+a2007=2，a2006•a2007=
．
∴a2006（1+q）=2 ①
a2006•a2006•q=
②
∴①2÷②：
=
，
∵q＞1，∴解得q=3．
∴a2008+a2009=a2006•q2+a2006•q3
=a2006•（1+q）•q2=2×32=18．
故答案为：18．
∵a2006和a2007是方程4x2-8x+3=0的两个根
∴a2006+a2007=2，a2006•a2007=
| 3 |
| 4 |
∴a2006（1+q）=2 ①
a2006•a2006•q=
| 3 |
| 4 |
∴①2÷②：
| (1+q)2 |
| q |
| 16 |
| 3 |
∵q＞1，∴解得q=3．
∴a2008+a2009=a2006•q2+a2006•q3
=a2006•（1+q）•q2=2×32=18．
故答案为：18．
点评：本题主要考查一元二次方程的根的分布与系数的关系以及等比数列的性质．在解决本题的过程中用到了整体代入的思想，当然本题也可以求出首项和公比再代入计算．
练习册系列答案
相关题目
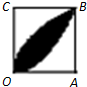在正方形OABC框格内有一块花纹（如图所示），花纹刚好过点O，B，经研究发现花纹边界是函数y=x2与