题目内容
14.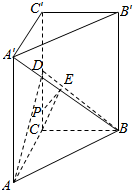 如图,在直三棱柱ABC-A′B′C′中,底面是等腰直角三角形,∠ACB=90°,侧棱AA′=2,BC=AC=1,D,E分别是CC′、A′B的中点.
如图,在直三棱柱ABC-A′B′C′中,底面是等腰直角三角形,∠ACB=90°,侧棱AA′=2,BC=AC=1,D,E分别是CC′、A′B的中点.(1)求异面直线CE与BD所成角的余弦值;
(2)在CC′上是否存在一点P,使得PE⊥平面ABD?若存在,请求出CP的值;若不存在,请说明理由.
分析 (1)以{$\overrightarrow{CA}$,$\overrightarrow{CB}$,$\overrightarrow{C{C}^{'}}$}为单位正交基底建立空间直角坐标系C-xyz,利用向量法能求出异面直线CE与BD所成角的余弦值.
(2)假设存在满足题意的点P,设P(0,0,t),求出平面ABD的法向量,利用向量法能求出在CC′上存在一点P,使得PE⊥平面ABD,并能求出此时CP的值.
解答 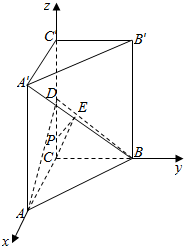 解:(1)以{$\overrightarrow{CA}$,$\overrightarrow{CB}$,$\overrightarrow{C{C}^{'}}$}为单位正交基底建立空间直角坐标系C-xyz,
解:(1)以{$\overrightarrow{CA}$,$\overrightarrow{CB}$,$\overrightarrow{C{C}^{'}}$}为单位正交基底建立空间直角坐标系C-xyz,
由已知得C(0,0,0),A(1,0,0),B(0,1,0),D(0,0,1),A′(1,0,2),
$\overrightarrow{BD}$=(0,-1,1),E($\frac{1}{2},\frac{1}{2},1$),$\overrightarrow{CE}$=($\frac{1}{2},\frac{1}{2},1$),
cos<$\overrightarrow{BD},\overrightarrow{CE}$>=$\frac{\overrightarrow{BD}•\overrightarrow{CE}}{|\overrightarrow{BD}|•|\overrightarrow{CE}|}$=$\frac{\frac{1}{2}}{\sqrt{2}×\frac{\sqrt{3}}{\sqrt{2}}}$=$\frac{\sqrt{3}}{6}$.
∴异面直线CE与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
(2)假设存在满足题意的点P,设P(0,0,t),
则$\overrightarrow{PE}=(\frac{1}{2},\frac{1}{2},1-t$),$\overrightarrow{AB}$=(-1,-1,0),$\overrightarrow{AD}$=(-1,0,1),
设平面ABD的法向量$\overrightarrow{m}$=(x,y,z),则$\left\{{\begin{array}{l}{\overrightarrow m•\overrightarrow{AB}=0}\\{\overrightarrow m•\overrightarrow{AD}=0}\end{array}}\right.$,即$\left\{\begin{array}{l}{-x+y=0}\\{-x+z=0}\end{array}\right.$,
不妨令x=1,可得平面ABD的法向量$\overrightarrow{m}$=(1,1,1),
若PE⊥平面ABD,则$\overrightarrow{PE}$∥$\overrightarrow{m}$,即$\frac{\frac{1}{2}}{1}=\frac{\frac{1}{2}}{1}=\frac{1-t}{1}$,解得t=$\frac{1}{2}$,故CP=$\frac{1}{2}$.
所以,在CC′上存在一点P,使得PE⊥平面ABD,此时CP=$\frac{1}{2}$.…(10分)
点评 本题考查异面直线所成角的余弦值的求法,考查满足条件的点的确定,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
| A. | (-1,0) | B. | [-2,0] | C. | (-∞,-2)∪(-1,0) | D. | [-2,+∞) |
| A. | $\frac{{2+\sqrt{2}}}{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | $\frac{{1+\sqrt{2}}}{2}$ |