题目内容
9.已知△ABC的内角A,B,C的对边分别为a,b,c,向量$\vec m=(sinA,a),\vec n=(1,sinB)$(1)当$\vec m•\vec n=2sinA$时,求b的值;
(2)当$\vec m∥\vec n$时,且$cosC=\frac{1}{2}a$,求tanA•tanB的值.
分析 (1)由题意得$\vec m•\vec n=sinA+asinB=2sinA$,即$\frac{a}{sinA}=\frac{1}{sinB}$,由正弦定理有:$\frac{a}{sinA}=\frac{b}{sinB}$,联立即可得解b的值.
(2)由平行条件得a=sinA•sinB,由$cosC=\frac{1}{2}a$,则可得$cosAcosB=\frac{1}{2}a$,联立即可得解.
解答 解:(1)由题意得:$\vec m•\vec n=sinA+asinB=2sinA$,…(2分)
即得$\frac{a}{sinA}=\frac{1}{sinB}$,
在三角形中由正弦定理有:$\frac{a}{sinA}=\frac{b}{sinB}$,…(4分)
由以上两式可知:b=1.…(6分)
(2)由平行条件得a=sinA•sinB,…(8分)
$cosC=-cos(A+B)=sinAsinB-cosAcosB=\frac{1}{2}a$,…(10分)
则可得到:$cosAcosB=\frac{1}{2}a$,…(12分)
∴$tanAtanB=\frac{sinAsinB}{cosAcosB}=2$.…(14分)
点评 本题主要考查了正弦定理,平面向量数量积的坐标运算,两角和的余弦函数公式的综合应用,考查了计算计算能力和转化思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.椭圆$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1的焦点坐标是( )
| A. | (0,±$\sqrt{5}$) | B. | (±$\sqrt{5}$,0) | C. | (0,±$\sqrt{13}$) | D. | (±$\sqrt{13}$,0) |
20.函数y=sinx+cos2x(x∈R)的值域为( )
| A. | [-$\frac{9}{8}$,2] | B. | [-2,$\frac{9}{8}$] | C. | [-$\frac{7}{8}$,2] | D. | [-2,$\frac{7}{8}$] |
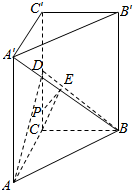 如图,在直三棱柱ABC-A′B′C′中,底面是等腰直角三角形,∠ACB=90°,侧棱AA′=2,BC=AC=1,D,E分别是CC′、A′B的中点.
如图,在直三棱柱ABC-A′B′C′中,底面是等腰直角三角形,∠ACB=90°,侧棱AA′=2,BC=AC=1,D,E分别是CC′、A′B的中点.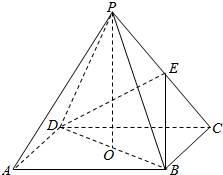 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.