题目内容
13.设a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,b=($\frac{1}{2}$)${\;}^{\frac{2}{3}}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则a,b,c的大小关系是( )| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵1>a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$>b=($\frac{1}{2}$)${\;}^{\frac{2}{3}}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$>$lo{g}_{\frac{1}{2}}\frac{1}{2}$=1,
则c>a>b,
故选:B.
点评 本题考查了指数函数对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
4.8名象棋选手进行单循环赛(即每两名选手比赛一场).规定两人对局胜者得2分,平局各得1分,负者得0分,并按总得分由高到低进行排序.比赛结束后,8名选手的得分各不相同,且第二名的得分与最后四名选手得分之和相等.则第二名选手的得分是( )
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
5.在△ABC中,a=1,b=$\sqrt{3}$,A=30°,则角C=( )
| A. | 60° | B. | 30°或90° | C. | 30° | D. | 60°或120° |
12.直三棱柱A1B1C1-ABC,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{30}}}{10}$ | C. | $\frac{{\sqrt{30}}}{15}$ | D. | $\frac{{\sqrt{15}}}{10}$ |
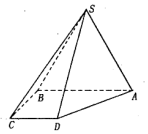 如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.
如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.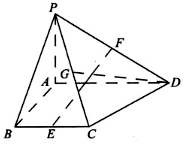 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.